[题目]如图.在平行四边形ABCD中.过对角线BD上一点P.作EF∥BC.HG∥AB.若四边形AEPH和四边形CFPG的面积分另为S1和S2.则S1与S2的大小关系为( )A．S1=S2 B．S1＞S2 C．S1＜S2 D．不能确定题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如图，在平行四边形ABCD中，过对角线BD上一点P，作EF∥BC，HG∥AB，若四边形AEPH和四边形CFPG的面积分另为S1和S2，则S1与S2的大小关系为（　　）

A．S1=S2 B．S1＞S2 C．S1＜S2 D．不能确定

【答案】A．

【解析】

试题分析：∵四边形ABCD是平行四边形，EF∥BC，HG∥AB，

∴AD=BC，AB=CD，AB∥GH∥CD，AD∥EF∥BC，

∴四边形GBEP、HPFD是平行四边形，

∵在△ABD和△CDB中，AB=CD，BD=BD，AD=BC，

∴△ABD≌△CDB，

即△ABD和△CDB的面积相等；

同理△BEP和△PGB的面积相等，△HPD和△FDP的面积相等，

∴四边形AEPH和四边形CFPG的面积相等，即S1=S2．

故选A．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

萌齐小升初强化模拟训练系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

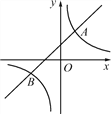
【题目】如图，直线y＝k1x＋b与双曲线y＝相交于A(1,2)、B(m，－1)两点．

(1)求直线和双曲线的解析式；

(2)若A1(x1，y1)、A2(x2，y2)、A3(x3，y3)为双曲线上的三点，且x1＜x2＜0＜x3，请直接写出y1、y2、y3的大小关系式；

(3)观察图象，请直接写出不等式k1x＋b＞的解集．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，请在下列四个关系中，选出两个恰当的关系作为条件，推出四边形ABCD是平行四边形，并予以证明．（写出一种即可）

关系：①AD∥BC，②AB=CD，③∠A=∠C，④∠B+∠C=180°．

已知：在四边形ABCD中，　　　　　　，　　　　　　；

求证：四边形ABCD是平行四边形．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知点P（2a﹣12，1﹣a）位于第三象限，点Q（x，y）位于第二象限且是由点P向上平移一定单位长度得到的．

（1）若点P的纵坐标为﹣3，试求出a的值；

（2）在（1）题的条件下，试求出符合条件的一个点Q的坐标；

（3）若点P的横、纵坐标都是整数，试求出a的值以及线段PQ长度的取值范围．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】邻边不相等的平行四边形纸片，剪去一个菱形，余下一个四边形，称为第一次操作；在余下的四边形纸片中再剪去一个菱形，又余下一个四边形，称为第二次操作；……依此类推，若第n次操作余下的四边形是菱形，则称原平行四边形为n阶准菱形．如图1，□ABCD中，若AB＝1，BC＝2，则□ABCD为1阶准菱形．

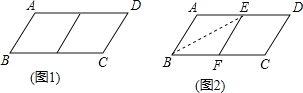
（1）判断与推理：

①邻边长分别为2和3的平行四边形是阶准菱形；

②小明为了剪去一个菱形，进行如下操作：如图2，把□ABCD沿BE折叠（点E在AD上），使点A落在BC边上的点F，得到四边形ABFE．请证明四边形ABEF是菱形．

（2）操作、探究与计算：

①已知□ABCD是邻边长分别为1，a（a＞1），且是3阶准菱形，请画出□ABCD及裁剪线的示意图，并在图形下方写出a的值；

②已知□ABCD的邻边长分别为a，b（a＞b），满足a＝6b＋r，b＝5r（r＞0），则□ABCD

是阶准菱形．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】在平行四边形ABCD中，分别以AD、BC为边向内作等边△ADE和等边△BCF，连接BE、DF．求证：四边形BEDF是平行四边形．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，已知抛物线y=ax2+bx+c（a≠0）的顶点坐标为（4，﹣ ），且与y轴交于点C（0，2），与x轴交于A，B两点（点A在点B的左边）．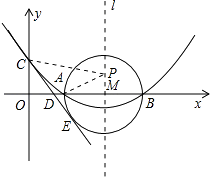

（1）求抛物线的解析式及A、B两点的坐标；
（2）在（1）中抛物线的对称轴l上是否存在一点P，使AP+CP的值最小？若存在，求AP+CP的最小值，若不存在，请说明理由；
（3）以AB为直径的⊙M相切于点E，CE交x轴于点D，求直线CE的解析式．