
已知AB是圆O的切线,切点为B,直线AO交圆O于C、D两点,CD=2,∠DAB=30°,动点P在直线AB上运动,PC交圆O于另一点Q.
(1)当点P运动到使Q、C两点重合时(如图1),求AP的长;
(2)点P在运动过程中,有几个位置(几种情况)使△CQD的面积为 ?(直接写出答案)
?(直接写出答案)
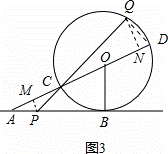
(3)当△CQD的面积为 ,且Q位于以CD为直径的上半圆,CQ>QD时(如图2),求AP的长.
,且Q位于以CD为直径的上半圆,CQ>QD时(如图2),求AP的长.

解:(1)∵AB与⊙O相切于点B,∴∠ABO=90°.
∵∠DAB=30°,OB= CD=
CD= ×2=1,
×2=1,
∴AO=2OB=2,AC=AO﹣CO=2﹣1=1.
当Q、C两点重合时,CP与⊙O相切于点C,如图1,
则有∠ACP=90°,
∴cos∠CAP= =
= =
= ,
,
解得AP= ;
;
(2)有4个位置使△CQD的面积为 .
.
提示:设点Q到CD的距离为h,
∵S△CQD= CD•h=
CD•h= ×2×h=
×2×h= ,
,
∴h= .
.
由于h=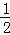 <1,结合图2可得:
<1,结合图2可得:
有4个位置使△CQD的面积为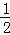 ;
;
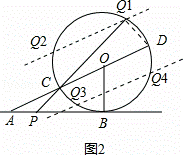
(3)过点Q作QN⊥CD于N,过点P作PM⊥CD于M,如图3.
∵S△CQD=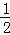 CD•QN=
CD•QN=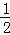 ×2×QN=
×2×QN=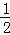 ,∴QN=
,∴QN=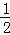 .
.
∵CD是⊙O的直径,QN⊥CD,
∴∠CQD=∠QND=∠QNC=90°,
∴∠CQN=90°﹣∠NQD=∠NDQ,
∴△QNC∽△DNQ,
∴ =
=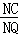 ,
,
∴QN2=CN•DN,
设CN=x,则有 =x(2﹣x),
=x(2﹣x),
整理得4x2﹣8x+1=0,
解得:x1=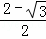 ,x2=
,x2=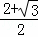 .
.
∵CQ>QD,∴x=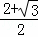 ,
,
∴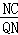 =2+
=2+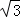 .
.
∵QN⊥CD,PM⊥CD,
∴∠PMC=∠QNC=90°.
∵∠MCP=∠NCQ,
∴△PMC∽△QNC,
∴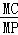 =
= =2+
=2+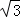 ,
,
∴MC=(2+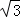 )MP.
)MP.
在Rt△AMP中,
tan∠MAP=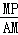 =tan30°=
=tan30°=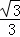 ,
,
∴AM=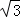 MP.
MP.
∵AC=AM+MC=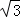 MP+(2+
MP+(2+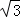 )MP=1,
)MP=1,
∴MP=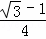 ,
,
∴AP=2MP= .
.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
如图,某校数学兴趣小组为测得大厦AB的高度,在大厦前的平地上选择一点C,测得大厦顶端A的仰角为30°,再向大厦方向前进80米,到达点D处(C、D、B三点在同一直线上),又测得大厦顶端A的仰角为45°,请你计算该大厦的高度.(精确到0.1米,参考数据: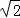 ≈1.414,
≈1.414,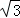 ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,利用一面墙(墙的长度不超过45米),用80米长的篱笆围成一共矩形场地
(1)若围成的矩形场地的面积为750m2,求矩形ABCD的长BC;
(2)能否使围成的矩形场地的面积为810m2?为什么?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com