
【题目】如图1,在平面直角坐标系,O为坐标原点,点A(﹣2,0),点B(0,2![]() ).
).

(1)直接写求∠BAO的度数;
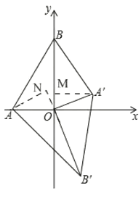
(2)如图1,将△AOB绕点O顺时针得△A′OB′,当A′恰好落在AB边上时,设△AB′O的面积为S1,△BA′O的面积为S2,S1与S2有何关系?为什么?
(3)若将△AOB绕点O顺时针旋转到如图2所示的位置,S1与S2的关系发生变化了吗?证明你的判断.
【答案】(1)∠BAO=60°;(2)S1=S2;理由见解析;(3)S1=S2不发生变化;证明见解析.
【解析】
(1)先求出OA,OB,再用锐角三角函数即可得出结论;
(2)根据旋转的性质和直角三角形的性质可证得OA'=AA'=AO=A'B,然后根据等边△AOA'的边AO、AA'上的高相等,即可得到S1=S2;
(3)根据旋转的性质可得BO=OB',AA'=OA',再求出∠AON=∠A'OM,然后利用“角角边”证明△AON和△A'OM全等,根据全等三角形对应边相等可得AN=A'M,然后利用等底等高的三角形的面积相等证明.
解:(1)∵A(2,0),B(0,![]() ),
),
∴OA=2,OB=![]() ,
,
在Rt△AOB中,tan∠BAO=![]() ,
,
∴∠BAO=60°;
(2)S1=S2;
理由:∵∠BAO=60°,∠AOB=90°,
∴∠ABO=30°,
∴OA'=OA=![]() AB,△AOA'是等边三角形,
AB,△AOA'是等边三角形,
∴OA'=AA'=AO=A'B,
∵∠B'A'O=60°,∠A'OA=60°,
∴B'A'∥AO,
根据等边三角形的性质可得,△AOA'的边AO、AA'上的高相等,即△AB′O中AO边上高和△BA′O中BA′边上的高相等,
∴△BA'O的面积和△AB'O的面积相等(等底等高的三角形的面积相等),
即S1=S2;
(3)S1=S2不发生变化;
理由:如图,过点A'作A'M⊥OB.过点A作AN⊥OB'交B'O的延长线于N,
∵△A'B'O是由△ABO绕点O旋转得到,
∴BO=OB',AO=OA',
∵∠AON+∠BON=90°,∠A'OM+∠BON=90°,
∴∠AON=∠A'OM,
在△AON和△A'OM中,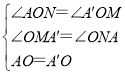 ,
,
∴△AON≌△A'OM(AAS),
∴AN=A'M,
∴△BOA'的面积和△AB'O的面积相等(等底等高的三角形的面积相等),
即S1=S2.


科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 在
在![]() 的
的![]() 边上,
边上,![]() 交
交![]() 于
于![]() ,
,![]() 交
交![]() 于
于![]() ,若添加条件________,则四边形
,若添加条件________,则四边形![]() 是矩形;若添加条件________,则四边形
是矩形;若添加条件________,则四边形![]() 是菱形;若添加条件________,则四边形
是菱形;若添加条件________,则四边形![]() 是正方形.
是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B是数轴上两点,点A对应的数是-2,点B对应的数是2. △ABC是等边三角形,D是AB中点. 点M在AC边上,且AM=3CM.
(1)求CD长.
(2)点P是CD上的动点,确定点P使得PM+PA的值最小,并求出PM+PA的最小值.
(3)过点M的直线与数轴交于点Q,且QM![]() .点Q对应的数是t,结合图形直接写出t的取值范围.
.点Q对应的数是t,结合图形直接写出t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD绕点C顺时针旋转90°后得到矩形CEFG,连接DG交EF于H,连接AF交DG于M;
(1)求证:AM=FM;
(2)若∠AMD=a.求证:![]() =cosα.
=cosα.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A是双曲线![]() 在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第四象限,随着点A的运动,点C的位置也不断变化,但点C始终在第四象限,且双曲线
在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第四象限,随着点A的运动,点C的位置也不断变化,但点C始终在第四象限,且双曲线![]() 始终经过点C,则k的值为_____.
始终经过点C,则k的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系xoy中,直线y=![]() x+
x+![]() 交x轴于点B,交y轴于点A,过点C(1,0)作x轴的垂线l,将直线l绕点C按逆时针方向旋转,旋转角为α(0°<α<180°).
交x轴于点B,交y轴于点A,过点C(1,0)作x轴的垂线l,将直线l绕点C按逆时针方向旋转,旋转角为α(0°<α<180°).

(1)当直线l与直线y=![]() x+
x+![]() 平行时,求出直线l的解析式;
平行时,求出直线l的解析式;
(2)若直线l经过点A,①求线段AC的长;②直接写出旋转角α的度数;
(3)若直线l在旋转过程中与y轴交于D点,当△ABD、△ACD、△BCD均为等腰三角形时,直接写出符合条件的旋转角α的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进甲、乙两种空调共50台.已知购进一台甲种空调比购进一台乙种空调进价少0.3万元;用20万元购进甲种空调数量是用40万元购进乙种空调数量的2倍.请解答下列问题:
(1)求甲、乙两种空调每台进价各是多少万元?
(2)若商场预计投入资金不少于10万元,且购进甲种空调至少31台,商场有哪几种购进方案?
(3)在(2)条件下,若甲种空调每台售价1100元,乙种空调每台售价4300元,甲、乙空调各有一台样机按八折出售,其余全部标价售出,商场从销售这50台空调获利中拿出2520元作为员工福利,其余利润恰好又可以购进以上空调共2台.请直接写出该商场购进这50台空调各几台.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() ,
,![]() ,
,![]() ,…都是等边三角形,其边长依次为2,4,6,…,其中点
,…都是等边三角形,其边长依次为2,4,6,…,其中点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,…,按此规律排下去,则点
,…,按此规律排下去,则点![]() 的坐标为( )
的坐标为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰![]() ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O、点C沿EF折叠后与点O重合,则∠CEF的度数是( )
ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O、点C沿EF折叠后与点O重合,则∠CEF的度数是( )
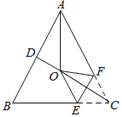
A. 60° B. 55° C. 50° D. 45°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com