
在Rt△ABC,∠C=90°,D为AB边上一点,点M、N分别在BC、AC边上,且DM⊥DN.作MF⊥AB于点F,NE⊥AB于点E.
(1)特殊验证:如图1,若AC=BC,且D为AB中点,求证:DM=DN,AE=DF;
(2)拓展探究:若AC≠BC.
①如图2,若D为AB中点,(1)中的两个结论有一个仍成立,请指出并加以证明;
②如图3,若BD=kAD,条件中“点M在BC边上”改为“点M在线段CB的延长线上”,其它条件不变,请探究AE与DF的数量关系并加以证明.
解:(1)证明:若AC=BC,则△ABC为等腰直角三角形,
如图,连接OD,则CD⊥AB,
又∵DM⊥DN,∴∠1=∠2。
在△AND与△CDM中, ,
,
∴△AND≌△CDM(ASA)。∴DM=DN。
∵∠4+∠1=90°,∠1+∠3=90°,∴∠4=∠3。
∵∠1+∠3=90°,∠3+∠5=90°,∴∠1=∠5。
在△NED与△DFM中, ,
,
∴△NED≌△DFM(ASA)。∴NE=DF。
∵△ANE为等腰直角三角形,∴AE=NE。∴AE=DF。
(2)①答:AE=DF。证明如下:
由(1)证明可知:△DEN∽△MFD,∴ ,即MF•EN=DE•DF。
,即MF•EN=DE•DF。
同理△AEN∽△MFB,∴ ,即MF•EN=AE•BF。
,即MF•EN=AE•BF。
∴DE•DF=AE•BF。∴(AD﹣AE)•DF=AE•(BD﹣DF)。
∴AD•DF=AE•BD。∴AE=DF。
②答:DF=kAE。证明如下:
由①同理可得:DE•DF=AE•BF,
∴(AE﹣AD)•DF=AE•(DF﹣BD)。∴AD•DF=AE•BD。
∵BD=kAD,∴DF=kAE。
解析试题分析:(1)如图,连接CD,证明△AND≌△CDM,可得DM=DN;证明△NED≌△DFM,可得DF=NE,从而得到AE=NE=DF。
(2)①若D为AB中点,则分别证明△DEN∽△MFD,△AEN∽△MFB,由线段比例关系可以证明AE=DF结论依然成立。
②若BD=kAD,证明思路与①类似。


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:解答题
如图,在梯形ABCD中,AD∥BC,AD=2,BC=4,点M是AD的中点,△MBC是等边三角形.
(1)求证:梯形ABCD是等腰梯形;
(2)动点P、Q分别在线段BC和MC上运动,且∠MPQ=60°保持不变.设PC=x,MQ=y,求y与x的函数关系式;
(3)在(2)中:
①当动点P、Q运动到何处时,以点P、M和点A、B、C、D中的两个点为顶点的四边形是平行四边形?并指出符合条件的平行四边形的个数;
②当y取最小值时,判断△PQC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知在△ABC中,∠ABC=90°,AB=3,BC=4.点Q是线段AC上的一个动点,过点Q作AC的垂线交线段AB(如图1)或线段AB的延长线(如图2)于点P.
(1)当点P在线段AB上时,求证:△APQ∽△ABC;
(2)当△PQB为等腰三角形时,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在△ABC中,∠C=90°,AC+BC=9,点O是斜边AB上一点,以O为圆心2为半径的圆分别与AC、BC相切于点D、E。
(1)求AC、BC的长;
(2)若AC=3,连接BD,求图中阴影部分的面积(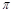 取3.14)。
取3.14)。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在正方形ABCD中,对角线AC与BD相交于点O,点E是BC上的一个动点,连接DE,交AC于点F.
(1)如图①,当 时,求
时,求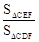 的值;
的值;
(2)如图②当DE平分∠CDB时,求证:AF=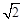 OA;
OA;
(3)如图③,当点E是BC的中点时,过点F作FG⊥BC于点G,求证:CG= BG.
BG.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
阅读理解:
如图1,在四边形ABCD的边AB上任取一点E(点E不与点A、点B重合),分别连接ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.解决问题:
(1)如图1,∠A=∠B=∠DEC=55°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图2,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图2中画出矩形ABCD的边AB上的一个强相似点E;
拓展探究:
(3)如图3,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处.若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB和BC的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,是一个照相机成像的示意图.
(1)如果像高MN是35mm,焦距是50mm,拍摄的景物高度AB是4.9m,拍摄点离景物有多远?
(2)如果要完整的拍摄高度是2m的景物,拍摄点离景物有4m,像高不变,则相机的焦距应调整为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com