
分析 (1)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与甲、乙、丙三名旅客在同一个站下车的情况,再利用概率公式即可求得答案;
(2)由(1)可求得甲、乙、丙三名旅客中至少有一人在老边站下车的有7种情况;然后利用概率公式求解即可求得答案.
解答 解:(1)画树状图得: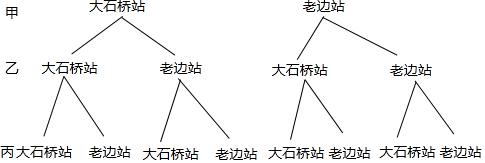
∵共有8种等可能的结果,甲、乙、丙三名旅客在同一个站下车的有2种情况,
∴甲、乙、丙三名旅客在同一个站下车的概率为:$\frac{2}{8}$=$\frac{1}{4}$;
(2)∵甲、乙、丙三名旅客中至少有一人在老边站下车的有7种情况;
∴甲、乙、丙三名旅客中至少有一人在老边站下车的概率为:$\frac{7}{8}$.
点评 此题考查了树状图法与列表法求概率.用到的知识点为:概率=所求情况数与总情况数之比.


科目:初中数学 来源: 题型:填空题
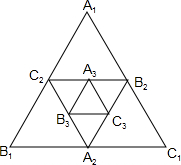 如图,小强作出边长为1的第1个等边△A1B1C1,计算器面积为S1,然后分别取△A1B1C1三边的中点A2、B2、C1,作出第2个等边△A2B2C2,计算其面积为S2,用同样的方法,作出第3个等边△A3B3C3,计算其面积为S3,按此规律进行下去,…,由此可得,第20个等边△A20B20C20的面积S20=$\frac{\sqrt{3}}{{4}^{20}}$.
如图,小强作出边长为1的第1个等边△A1B1C1,计算器面积为S1,然后分别取△A1B1C1三边的中点A2、B2、C1,作出第2个等边△A2B2C2,计算其面积为S2,用同样的方法,作出第3个等边△A3B3C3,计算其面积为S3,按此规律进行下去,…,由此可得,第20个等边△A20B20C20的面积S20=$\frac{\sqrt{3}}{{4}^{20}}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≥5 | B. | 0≤x≤5 | C. | x≥0 | D. | x为任意实数 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
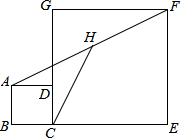 如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=4,H是AF的中点,那么CH的长是$\frac{1}{2}\sqrt{34}$.
如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=4,H是AF的中点,那么CH的长是$\frac{1}{2}\sqrt{34}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,扇形AOB中,OA=10,∠AOB=36°,若固定B点,将此扇形按顺时针方向旋转,得一新扇形O′BA′,其中A点在BO′上,则O点旋转至O′点所经过的路径的长度为4π.(结果保留π)
如图,扇形AOB中,OA=10,∠AOB=36°,若固定B点,将此扇形按顺时针方向旋转,得一新扇形O′BA′,其中A点在BO′上,则O点旋转至O′点所经过的路径的长度为4π.(结果保留π)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com