
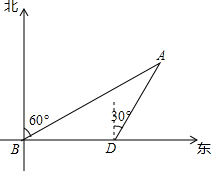
 如图,海中有一小岛A,它的周围10海里内有暗礁,渔船由西向东航行.在B点测得小岛A在北偏东60°方向,再航行12海里到达D点,这时测得小岛A在北偏东30°方向.如果渔船不改变航向,继续向东航行,有没有触礁的危险?
如图,海中有一小岛A,它的周围10海里内有暗礁,渔船由西向东航行.在B点测得小岛A在北偏东60°方向,再航行12海里到达D点,这时测得小岛A在北偏东30°方向.如果渔船不改变航向,继续向东航行,有没有触礁的危险? 分析 作AM⊥BD于M,首先证明BD=AD=12,在RT△ADM中求出AM与10比较,AM大于等于10海里没有危险,AM小于10有危险.
解答  解:如图作AM⊥BD于M.
解:如图作AM⊥BD于M.
∵∠ABD=30°,∠ADM=60°,∠ADM=∠ABD+∠BAD,
∴∠DBA=∠DAB=30°,
∴DB=DA=12,
在RT△ADM中,∵∠AMD=90°,AD=12,∠DAM=30°,
∴DM=$\frac{1}{2}$AD=6,AM=$\sqrt{3}$DM=6$\sqrt{3}$≈10.4>10,
∴渔船不改变航向,继续向东航行,没有触礁的危险.
点评 本题考查解直角三角形、方向角、特殊角的三角函数等知识,解题的关键是添加辅助线构造直角三角形,把实际问题转化为解直角三角形问题,属于中考常考题型.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:解答题
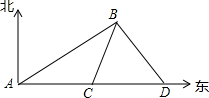 如图,某船在海上航行,在A处观测到灯塔B在北偏东60°方向上,该船以每小时15海里的速度向东航行到达C处,观测到灯塔B在北偏东30°方向上,继续向东航行到D处,观测到灯塔B在北偏西30°方向上,当该船到达D处时恰与灯塔B相距60海里.
如图,某船在海上航行,在A处观测到灯塔B在北偏东60°方向上,该船以每小时15海里的速度向东航行到达C处,观测到灯塔B在北偏东30°方向上,继续向东航行到D处,观测到灯塔B在北偏西30°方向上,当该船到达D处时恰与灯塔B相距60海里.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
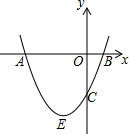 如图,抛物线y=x2+bx+c与y轴交于点C,与x轴交于点A,B,点A在点B的左侧,点A的坐标为A(-3,0),且AB=4.
如图,抛物线y=x2+bx+c与y轴交于点C,与x轴交于点A,B,点A在点B的左侧,点A的坐标为A(-3,0),且AB=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
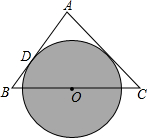 如图,在△ABC中,AB=AC,O是BC的中点,以O为圆心的⊙O切AB于D,求证:AC是⊙O的切线.(提示:证明切线的基本思路:不知共点,作垂直,证半径)
如图,在△ABC中,AB=AC,O是BC的中点,以O为圆心的⊙O切AB于D,求证:AC是⊙O的切线.(提示:证明切线的基本思路:不知共点,作垂直,证半径)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
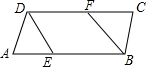 完成下面证明
完成下面证明查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com