
 �������֤��
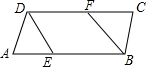
�������֤������ �ȸ��ݽ�ƽ���ߵ����ʵó���ABF=$\frac{1}{2}$��ABC����CDE=$\frac{1}{2}$��ADC��������֪�����ɵó���ABF=��CDE��ͬ���ɵá�AED=��CDE����ƽ���ߵ��ж������ó�AB��CD������ƽ���ߵ����ʼ��ɵó����ۣ�
��� ֤��������BF��DEƽ�֡�ABC����ADC ����֪����
��$��ABF=\frac{1}{2}$��ABC��$��CDE=\frac{1}{2}$��ADC����ƽ���ߵĶ��壩��
�ߡ�ABC=��ADC ����֪����
���ABF=��CDE ��������������
�ߡ�AED=��ABF ����֪����
���AED=��CDE ��������������
��AB��CD ���ڴ�����ȣ���ֱ��ƽ�У���
���A+��ADC=180�㣬��C+��ABC=180�㣨��ֱ��ƽ�У�ͬ���ڽǻ�������
�ߡ�ABC=��ADC ����֪����
���A=��C��������������
�ʴ�Ϊ����֪����ƽ���ߵĶ��壬��֪��������������֪�������������ڴ�����ȣ���ֱ��ƽ�У���ֱ��ƽ�У�ͬ���ڽǻ�������֪������������
���� ���⿼�����ƽ���ߵ��ж��������õ���֪ʶ��Ϊ���ڴ�����ȣ���ֱ��ƽ�У�


 ����ȫ���ִʾ��ƪ��ϵ�д�
����ȫ���ִʾ��ƪ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
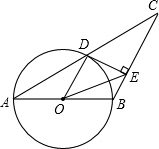 ��ͼ����֪������ABC��AB=BC����ABΪֱ����Բ��AC�ڵ�D��������D����O�����߽�BC�ڵ�E����CD=10��CE=8��
��ͼ����֪������ABC��AB=BC����ABΪֱ����Բ��AC�ڵ�D��������D����O�����߽�BC�ڵ�E����CD=10��CE=8���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
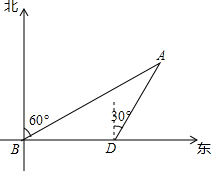 ��ͼ��������һС��A��������Χ10�������а������洬�������У���B����С��A�ڱ�ƫ��60�㷽���ٺ���12���ﵽ��D�㣬��ʱ���С��A�ڱ�ƫ��30�㷽������洬���ı亽�������У���û�д�����Σ�գ�
��ͼ��������һС��A��������Χ10�������а������洬�������У���B����С��A�ڱ�ƫ��60�㷽���ٺ���12���ﵽ��D�㣬��ʱ���С��A�ڱ�ƫ��30�㷽������洬���ı亽�������У���û�д�����Σ�գ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
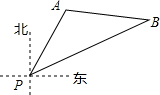 ��ͼ��һ�Һ���λ�ڵ���P�ı�ƫ��30�㷽�������20�����A������������������һ��ʱ�����λ�ڵ���P�ı�ƫ��60�㷽���ϵ�B�������ʱ�ִ�������ľ���BPΪ20$\sqrt{3}$���
��ͼ��һ�Һ���λ�ڵ���P�ı�ƫ��30�㷽�������20�����A������������������һ��ʱ�����λ�ڵ���P�ı�ƫ��60�㷽���ϵ�B�������ʱ�ִ�������ľ���BPΪ20$\sqrt{3}$����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
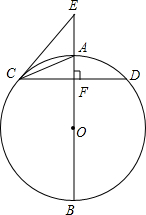 ��ͼ����֪ABΪ��O��ֱ������CD��AB������ΪF��EΪBA�ӳ����ϵ�һ�㣬����CE��CA����ECA=��ACD��
��ͼ����֪ABΪ��O��ֱ������CD��AB������ΪF��EΪBA�ӳ����ϵ�һ�㣬����CE��CA����ECA=��ACD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com