
【题目】下列命题的逆命题为假命题的是( )
A.如果一元二次方程![]() 没有实数根,那么
没有实数根,那么![]() .
.
B.线段垂直平分线上任意一点到这条线段两个端点的距离相等.
C.如果两个数相等,那么它们的平方相等.
D.直角三角形两条直角边的平方和等于斜边的平方.
科目:初中数学 来源: 题型:
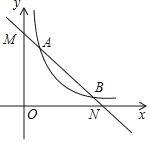
【题目】如图,在平面直角坐标中,点O是坐标原点,一次函数y1=kx+b与反比例函数y2=![]() 的图象交于A(1,m)、B(n,1)两点.
的图象交于A(1,m)、B(n,1)两点.
(1)求直线AB的解析式;
(2)根据图象写出当y1>y2时,x的取值范围;
(3)若点P在y轴上,求PA+PB的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
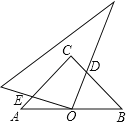
【题目】如图,在Rt△ABC中,∠C=90°.点O是AB的中点,边AC=6,将边长足够大的三角板的直角顶点放在点O处,将三角板绕点0旋转,始终保持三角板的直角边与AC相交,交点为点E,另条直角边与BC相交,交点为D,则等腰直角三角板的直角边被三角板覆盖部分的两条线段CD与CE的长度之和为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一条抛物线![]() 与
与![]() 轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
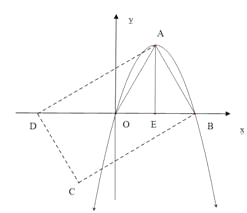
(1)“抛物线三角形”一定是 三角形;
(2)若抛物线![]() 的“抛物线三角形”是等腰直角三角形,求
的“抛物线三角形”是等腰直角三角形,求![]() 的值;
的值;
(3)如图,△![]() 是抛物线
是抛物线![]() 的“抛物线三角形”,是否存在以原点
的“抛物线三角形”,是否存在以原点![]() 为对称中心的矩形
为对称中心的矩形![]() ?若存在,求出过
?若存在,求出过![]() 三点的抛物线的表达式;若不存在,说明理由.
三点的抛物线的表达式;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,自左至右,第1个图由1个正六边形、6个正方形和6个等边三角形组成;第2个图由2个正六边形、11个正方形和10个等边三角形组成;第3个图由3个正六边形、16个正方形和14个等边三角形组成;…按照此规律,第![]() 个图中正方形和等边三角形的个数之和为 个.
个图中正方形和等边三角形的个数之和为 个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以∠AOB的顶点O为圆心,适当长为半径画弧,交OA于点C,交OB于点D.再分别以点C、D为圆心,大于![]() CD的长为半径画弧,两弧在∠AOB内部交于点E,过点E作射线OE,连接CD.则下列说法错误的是
CD的长为半径画弧,两弧在∠AOB内部交于点E,过点E作射线OE,连接CD.则下列说法错误的是

A.射线OE是∠AOB的平分线
B.△COD是等腰三角形
C.C、D两点关于OE所在直线对称
D.O、E两点关于CD所在直线对称
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】物华小区停车场去年收费标准如下:中型汽车的停车费为600元/辆,小型汽车的停车费为400元/辆,停满车辆时能收停车费23000元,今年收费标准上调为:中型汽车的停车费为1000元/辆,小型汽车的停车费为600元/辆,若该小区停车场容纳的车辆数没有变化,今年比去年多收取停车费13000元.
(1)该停车场去年能停中、小型汽车各多少辆?
(2)今年该小区因建筑需要缩小了停车场的面积,停车总数减少了11辆,设该停车场今年能停中型汽车![]() 辆,小型汽车有
辆,小型汽车有![]() 辆,停车场收取的总停车费为
辆,停车场收取的总停车费为![]() 元,请求出
元,请求出![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(3)在(2)的条件下,若今年该停车场停满车辆时小型汽车的数量不超过中型汽车的2倍,则今年该停车场最少能收取的停车费共多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高速公路有![]() 的路段需要维修,拟安排甲、乙两个工程队合作完成,规定工期不得超过一个月(30天) ,已知甲队每天维修公路的长度是乙队每天维修公路长度的2倍,并且在各自独立完成长度为
的路段需要维修,拟安排甲、乙两个工程队合作完成,规定工期不得超过一个月(30天) ,已知甲队每天维修公路的长度是乙队每天维修公路长度的2倍,并且在各自独立完成长度为![]() 公路的维修时,甲队比乙队少用6天
公路的维修时,甲队比乙队少用6天
(1)求甲乙两工程队每天能完成维修公路的长度分别是多少![]()
(2)若甲队的工程费用为每天2万元,乙队每天的工程费用为1.2万元,15 天后乙队另有任务,余下工程由甲队完成,请你判断能否在规定的工期完成且总费用不超过80万元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com