练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，自左至右，第1个图由1个正六边形、6个正方形和6个等边三角形组成；第2个图由2个正六边形、11个正方形和10个等边三角形组成；第3个图由3个正六边形、16个正方形和14个等边三角形组成；…按照此规律，第个图中正方形和等边三角形的个数之和为 个.

    【答案】9n+3

    【解析】

    试题分析：∵第1个图由1个正六边形、6个正方形和6个等边三角形组成，

    ∴正方形和等边三角形的和=6+6=12=9+3；

    ∵第2个图由11个正方形和10个等边三角形组成，

    ∴正方形和等边三角形的和=11+10=21=9×2+3；

    ∵第3个图由16个正方形和14个等边三角形组成，

    ∴正方形和等边三角形的和=16+14=30=9×3+3，

    …，

    ∴第n个图中正方形和等边三角形的个数之和=9n+3．

    故答案为：9n+3．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某校课外兴趣小组从某市七年级学生中抽取2000人做了如下问卷调查，并将调查结果绘制成如图所示的两幅统计图．

    问卷

    你平时喝饮料吗？(　　)

    A．不喝 　　　B．喝

    请选择B选项的同学回答下面问题：

    请您减少喝饮料的数量，将节省下来的钱捐给希望工程，您愿意平均每月少喝(　　)

    A．0瓶 　　　B．1瓶

    C．2瓶 　　　D．2瓶以上

    根据上述信息，解答下列问题：

    (1)求条形图中n的值．

    (2)如果每瓶饮料平均3元钱，“少喝2瓶以上”按少喝3瓶计算：

    ①这2000名学生一个月少喝饮料能节省多少钱捐给希望工程？

    ②按上述统计结果估计，该市七年级6万名学生一个月少喝饮料大约能节省多少钱捐给希望工程？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列各题计算正确的是 ( )

    A. (ab﹣1)·(﹣4ab2)=﹣4a2b3﹣4ab2 B. (3x2+xy﹣y2)·3x2=9x4+3x3y﹣y2

    C. (﹣3a)·(a2﹣2a+1)=﹣3a3+6a2 D. (﹣2x)·(3x2﹣4x﹣2)=﹣6x3+8x2+4x

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】类比梯形的定义，我们定义：有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”．

    （1）已知：如图1，四边形ABCD是“等对角四边形”，∠A≠∠C，∠A=70°，∠B=80°．求∠C，∠D的度数．
    （2）在探究“等对角四边形”性质时：
    ①小红画了一个“等对角四边形”ABCD（如图2），其中∠ABC=∠ADC，AB=AD，此时她发现CB=CD成立．请你证明此结论；
    ②由此小红猜想：“对于任意‘等对角四边形’，当一组邻边相等时，另一组邻边也相等”．你认为她的猜想正确吗？若正确，请证明；若不正确，请举出反例．
    （3）已知：在“等对角四边形”ABCD中，∠DAB=60°，∠ABC=90°，AB=5，AD=4．求对角线AC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点C在⊙O的直径AB上，AB=6，AC=1．点P为⊙O上的任意一点，当∠OPC取最大值时，则△OCP的面积为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知某市2013年企业用水量x（吨）与该月应交的水费y（元）之间的函数关系如图所示．
    （1）当x≥50时，求y关于x的函数关系式；
    （2）若某企业2013年10月份的水费为620元，求该企业2013年10月份的用水量；
    （3）为贯彻省委“五水共治”发展战略，鼓励企业节约用水，该市自2014年1月开始对月用水量超过80吨的企业加收污水处理费，规定：若企业月用水量x超过80吨，则除按2013年收费标准收取水费外，超过80吨部分每吨另加收 元，若某企业2014年3月份的水费和污水处理费共600元，求这个企业该月的用水量．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】学校为统筹安排大课间体育活动，在各班随机选取了一部分学生，分成四类活动：“篮球”、“羽毛球”、“乒乓球”、“其他”进行调查，整理收集到的数据，绘制成如下的两幅统计图．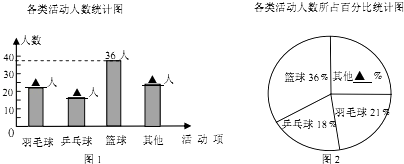
    （1）学校采用的调查方式是；学校共选取了名学生；
    （2）补全统计图中的数据：条形统计图中羽毛球人、乒乓球人、其他人、扇形统计图中其他%；
    （3）该校共有1100名学生，请估计喜欢“篮球”的学生人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】设y=kx，是否存在实数k，使得代数式（x2﹣y2）（4x2﹣y2）+3x2（4x2﹣y2）能化简为x4？若能，请求出所有满足条件的k的值；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在同一直角坐标系中，直线y=﹣x+3与y=3x﹣5相交于C点，分别与x轴交于A、B两点．P、Q分别为直线y=﹣x+3与y=3x﹣5上的点．
    （1）求△ABC的面积；
    （2）若P、Q关于原点成中心对称，求P点的坐标；
    （3）若△QPC≌△ABC，求Q点的坐标．

    查看答案和解析>>

    同步练习册答案