
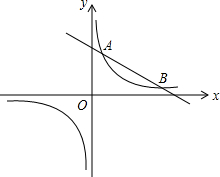
 ��ͼ��˫����y=$\frac{k}{x}$��k��0����ֱ��y=-$\frac{1}{2}$x+4�ཻ��A��B���㣮
��ͼ��˫����y=$\frac{k}{x}$��k��0����ֱ��y=-$\frac{1}{2}$x+4�ཻ��A��B���㣮���� ��1����y=$\frac{6}{x}$��y=-$\frac{1}{2}$x+4��������ɷ����飬�ⷽ���鼴����⣻
��2�������е���������壬��֪��$\frac{{x}_{1}+{x}_{2}}{2}$��$\frac{{y}_{1}+{y}_{2}}{2}$�����߶�MN���е㣬���ͼ����������������ۣ��ٵ�M��N��P���ڵ�һ���ޣ��ڵ�M��N��P���ڵ������ޣ�
��� �⣺��1���ⷽ����$\left\{\begin{array}{l}{y=\frac{6}{x}}\\{y=-\frac{1}{2}x+4}\end{array}\right.$����$\left\{\begin{array}{l}{{x}_{1}=2}\\{{y}_{1}=3}\end{array}\right.$��$\left\{\begin{array}{l}{{x}_{2}=6}\\{{y}_{2}=1}\end{array}\right.$��
���Ե�A������Ϊ��2��3������B������Ϊ��6��1����
��2������˫����y=$\frac{k}{x}$��k��0����ͬһ֧��������M��x1��y1����N��x2��y2����P��$\frac{{x}_{1}+{x}_{2}}{2}$��y0����
����$\frac{{x}_{1}+{x}_{2}}{2}$��$\frac{{y}_{1}+{y}_{2}}{2}$�����߶�MN���е㣬
��ɷ���������������ۣ�
�������M��N��P���ڵ�һ���ޣ���ôy0��$\frac{{y}_{1}+{y}_{2}}{2}$��
�������M��N��P���ڵ������ޣ���ôy0��$\frac{{y}_{1}+{y}_{2}}{2}$��
���� ���⿼���˷�����������һ�κ����Ľ������⣺����������һ�κ����Ľ������꣬������������ϵʽ�����ɷ�������⣬���������н��������н��㣬�������⣬���������㣮Ҳ�������߶ε��е����깫ʽ�Լ����ν�ϵ�˼�룮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
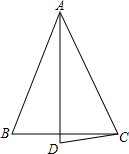 ��ͼ���ڡ�ABC�У���B=��C����D�ڡ�ABC�⣬��ADC=��ACD��
��ͼ���ڡ�ABC�У���B=��C����D�ڡ�ABC�⣬��ADC=��ACD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
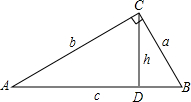 СҶ�Ӽ����еõ������Ľ��ۣ���ͼ����Rt��ABC�У���ACB=90�㣬CD��AB������ΪD����BC=a��AC=b��AB=c��CD=h�����е�ʽ$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=$\frac{1}{{h}^{2}}$�����������ж�СҶ�Ľ����Ƿ���ȷ������ȷ�������֤����������ȷ����˵�����ɣ�
СҶ�Ӽ����еõ������Ľ��ۣ���ͼ����Rt��ABC�У���ACB=90�㣬CD��AB������ΪD����BC=a��AC=b��AB=c��CD=h�����е�ʽ$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=$\frac{1}{{h}^{2}}$�����������ж�СҶ�Ľ����Ƿ���ȷ������ȷ�������֤����������ȷ����˵�����ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
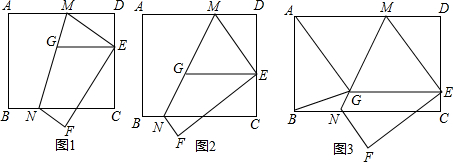
 ��ͼ��ֱ��a��b��ֱ��c���أ����������������в��ܵó�����a��b���ǣ�������
��ͼ��ֱ��a��b��ֱ��c���أ����������������в��ܵó�����a��b���ǣ�������| A�� | ��1=��3 | B�� | ��1=��4 | C�� | ��1=��2 | D�� | ��1+��2=180�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com