
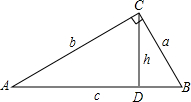
 小叶从计算中得到这样的结论:如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.设BC=a,AC=b,AB=c,CD=h,则有等式$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=$\frac{1}{{h}^{2}}$成立.请你判断小叶的结论是否正确?若正确,请给予证明;若不正确,请说明理由.
小叶从计算中得到这样的结论:如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.设BC=a,AC=b,AB=c,CD=h,则有等式$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=$\frac{1}{{h}^{2}}$成立.请你判断小叶的结论是否正确?若正确,请给予证明;若不正确,请说明理由. 分析 根据三角形面积公式和比例的性质求出$\frac{{c}^{2}}{{a}^{2}{b}^{2}}$=$\frac{1}{{h}^{2}}$,根据勾股定理得出a2+b2=c2,即可得出答案.
解答 正确,
证明:∵由三角形面积公式得:S△ABC=$\frac{1}{2}$ab=$\frac{1}{2}$ch,
∴ab=ch,
即a2b2=c2h2,
∴$\frac{1}{{a}^{2}{b}^{2}}$=$\frac{1}{{c}^{2}{h}^{2}}$,
∴$\frac{{c}^{2}}{{a}^{2}{b}^{2}}$=$\frac{1}{{h}^{2}}$
由勾股定理得:a2+b2=c2,
∴$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=$\frac{{b}^{2}+{a}^{2}}{{a}^{2}{b}^{2}}$=$\frac{{c}^{2}}{{a}^{2}{b}^{2}}$,
∴$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=$\frac{1}{{h}^{2}}$,
即小叶的结论正确.
点评 本题考查了勾股定理和三角形的面积公式的应用,能灵活运用定理进行推理是解此题的关键.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
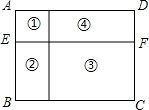 如图,要用60m的篱笆在一块足够大的空地上围出四个花园,已知①号花园为正方形,且④号花园的周长等于①号和②号花园周长之和.设CD的长为xm,②号花园的面积为ym2.
如图,要用60m的篱笆在一块足够大的空地上围出四个花园,已知①号花园为正方形,且④号花园的周长等于①号和②号花园周长之和.设CD的长为xm,②号花园的面积为ym2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
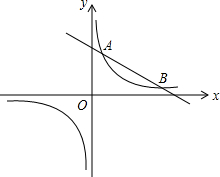 如图,双曲线y=$\frac{k}{x}$(k>0)与直线y=-$\frac{1}{2}$x+4相交于A,B两点.
如图,双曲线y=$\frac{k}{x}$(k>0)与直线y=-$\frac{1}{2}$x+4相交于A,B两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com