
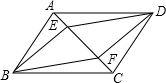
 已知:如图,在四边形ABCD中,AB=CD,BC=AD,点E、F在AC上,且AF=CE.求证:四边形BEDF是平行四边形.
已知:如图,在四边形ABCD中,AB=CD,BC=AD,点E、F在AC上,且AF=CE.求证:四边形BEDF是平行四边形. 科目:初中数学 来源: 题型:解答题
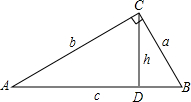 小叶从计算中得到这样的结论:如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.设BC=a,AC=b,AB=c,CD=h,则有等式$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=$\frac{1}{{h}^{2}}$成立.请你判断小叶的结论是否正确?若正确,请给予证明;若不正确,请说明理由.
小叶从计算中得到这样的结论:如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.设BC=a,AC=b,AB=c,CD=h,则有等式$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=$\frac{1}{{h}^{2}}$成立.请你判断小叶的结论是否正确?若正确,请给予证明;若不正确,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
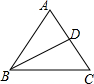 在△ABC中,AB=AC=5,BC=6,BD平分∠ABC.将△ABD沿BD折叠,点A落在A′处,则△DA′C的面积是$\frac{12}{11}$.
在△ABC中,AB=AC=5,BC=6,BD平分∠ABC.将△ABD沿BD折叠,点A落在A′处,则△DA′C的面积是$\frac{12}{11}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com