
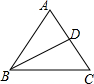
 在△ABC中,AB=AC=5,BC=6,BD平分∠ABC.将△ABD沿BD折叠,点A落在A′处,则△DA′C的面积是$\frac{12}{11}$.
在△ABC中,AB=AC=5,BC=6,BD平分∠ABC.将△ABD沿BD折叠,点A落在A′处,则△DA′C的面积是$\frac{12}{11}$. 分析 如图,作辅助线;首先运用勾股定理求出AE的长度,进而求出△ABC的面积;求出△DBA′、△CDA′的面积之比;证明△ABD、△A′BD的面积相等,即可解决问题.
解答  解:如图,过点A作AE⊥BC于点E;
解:如图,过点A作AE⊥BC于点E;
∵AB=AC,
∴BE=CE=3;由勾股定理得:
AB2=AE2+BE2,而AB=5,
∴AE=4,S△ABC=$\frac{1}{2}$×6×4=12;
由题意得:S△ABD=S${\;}_{△{A}^{′}BD}$,A′B=AB=5,
∴CA′=6-5=1,
∴$\frac{{S}_{△{A}^{′}BD}}{{S}_{△D{A}^{′}C}}$=$\frac{BA′}{CA′}$=$\frac{5}{1}$,
∴若设S${\;}_{△D{A}^{′}C}$=x,则S△ABD=S${\;}_{△{A}^{′}BD}$=5x,
故x+5x+5x=12,
∴x=$\frac{12}{11}$,
故答案为$\frac{12}{11}$.
点评 该题主要考查了翻折变换的性质、等腰三角形的性质、勾股定理等几何知识点及其应用问题;解题的方法是作辅助线,构造直角三角形;解题的关键是灵活运用翻折变换的性质来分析、判断、解答.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
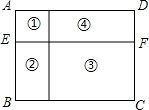 如图,要用60m的篱笆在一块足够大的空地上围出四个花园,已知①号花园为正方形,且④号花园的周长等于①号和②号花园周长之和.设CD的长为xm,②号花园的面积为ym2.
如图,要用60m的篱笆在一块足够大的空地上围出四个花园,已知①号花园为正方形,且④号花园的周长等于①号和②号花园周长之和.设CD的长为xm,②号花园的面积为ym2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
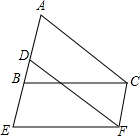 如图,将三角形ABC沿射线AB的方向平移2个单位到三角形DEF的位置,连接CF,点A,B,C的对应点分别是点D,E,F.
如图,将三角形ABC沿射线AB的方向平移2个单位到三角形DEF的位置,连接CF,点A,B,C的对应点分别是点D,E,F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com