
| A. | 45° | B. | 75° | C. | 45°或15°或75° | D. | 60° |
分析 作出图形,分①点A是顶点时,根据等腰三角形三线合一的性质可得BD=CD,从而得到AD=BD=CD,再利用等边对等角的性质可得∠B=∠BAD,然后利用直角三角形两锐角互余求解即可;
②点A是底角顶点时,根据直角三角形30°角所对的直角边等于斜边的一半求出∠C=30°,然后再根据等腰三角形两底角相等求解即可.
解答 解:①如图1,点A是顶点时,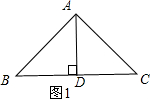
∵AB=AC,AD⊥BC,
∴BD=CD,
∵AD=$\frac{1}{2}$BC,
∴AD=BD=CD,
在Rt△ABD中,∠B=∠BAD=$\frac{1}{2}$(180°-90°)=45°;
②如图2,点A是底角顶点,且AD在△ABC外部时,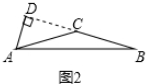
∵AD=$\frac{1}{2}$BC,AC=BC,
∴AD=$\frac{1}{2}$AC,
∴∠ACD=30°,
∴∠BAC=∠ABC=$\frac{1}{2}$×30°=15°;
②如图2,点A是底角顶点,且AD在△ABC内部时,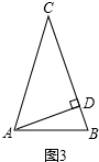
∵AD=$\frac{1}{2}$BC,AC=BC,
∴AD=$\frac{1}{2}$AC,
∴∠C=30°,
∴∠BAC=∠ABC=$\frac{1}{2}$(180°-30°)=75°;
综上所述,△ABC底角的度数为45°或15°或75°.
故选C.
点评 本题考查了30°角所对的直角边等于斜边的一半的性质,等腰三角形的两底角相等的性质,以及三角形的一个外角等于与它不相邻的两个内角的和的性质,难点在于要分情况讨论求解.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:解答题
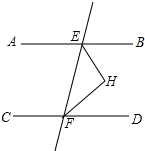 如图,已知AB∥CD,EF与两平行线分别交于点E、F,EH平分∠BEF,FH平分∠EFD,EH与FH交于点H.求证:△EFH是直角三角形.
如图,已知AB∥CD,EF与两平行线分别交于点E、F,EH平分∠BEF,FH平分∠EFD,EH与FH交于点H.求证:△EFH是直角三角形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
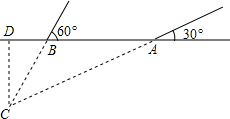 2014年3月,某海域发生航班失联事件,我海事救援部门用高频海洋探测仪进行海上搜救,分别在A、B两个探测点探测到C处是信号发射点,已知A、B两点相距400m,探测线与海平面的夹角分别是30°和60°,若CD的长是点C到海平面的最短距离.
2014年3月,某海域发生航班失联事件,我海事救援部门用高频海洋探测仪进行海上搜救,分别在A、B两个探测点探测到C处是信号发射点,已知A、B两点相距400m,探测线与海平面的夹角分别是30°和60°,若CD的长是点C到海平面的最短距离.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
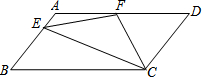 如图,在?ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论:(1)∠DCF=$\frac{1}{2}$∠BCD,(2)EF=CF;(3)S△BEC=2S△CEF;(4)∠DFE=3∠AEF,其中正确结论的个数是( )
如图,在?ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论:(1)∠DCF=$\frac{1}{2}$∠BCD,(2)EF=CF;(3)S△BEC=2S△CEF;(4)∠DFE=3∠AEF,其中正确结论的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{x{y}^{2}}{5}$的系数是-5 | B. | $\frac{t}{2}$是分式 | ||
| C. | $\frac{\sqrt{2}}{2}$不是分数 | D. | -22xyz2的次数是6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com