
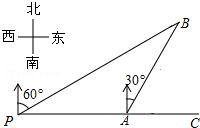
 如图,某船从观测站P以每小时4海里的速度航行1小时到达港口A,再沿北偏东30°方向航行一段距离后到达港口B处,此时从观测点P处测得该船位于北偏东60°的方向,求港口B与观测站P之间的距离.
如图,某船从观测站P以每小时4海里的速度航行1小时到达港口A,再沿北偏东30°方向航行一段距离后到达港口B处,此时从观测点P处测得该船位于北偏东60°的方向,求港口B与观测站P之间的距离. 分析 如图,过点B作BE⊥PC于E.通过解直角△ABE得到BE=AE•tan60°=$\sqrt{3}$AE,通过解直角△BPE得到BE=PE•tan30°=$\frac{\sqrt{3}}{3}$PE=$\frac{\sqrt{3}}{3}$(4+AE),据此列出关于AE的方程,由此求得AE的长度,然后通过解△BPE得到PB的长度.
解答 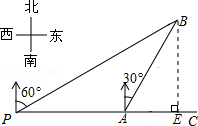 解:如图,过点B作BE⊥PC于E.
解:如图,过点B作BE⊥PC于E.
在直角△ABE中,∠BAE=60°,则BE=AE•tan60°=$\sqrt{3}$AE.
在直角△BPE中,∠BPE=30°,则BE=PE•tan30°=$\frac{\sqrt{3}}{3}$PE=$\frac{\sqrt{3}}{3}$(4+AE),
所以,$\sqrt{3}$AE=$\frac{\sqrt{3}}{3}$(4+AE),
所以,AE=2海里.
所以,PE=6海里,
所以,BP=$\frac{PE}{cos30°}$=$\frac{6}{\frac{\sqrt{3}}{2}}$=4$\sqrt{3}$(海里).
答:港口B与观测站P之间的距离是4$\sqrt{3}$海里.
点评 本题考查了解直角三角形的应用--方向角问题.难度适中,作出辅助线构造直角三角形是解题的关键.


科目:初中数学 来源: 题型:解答题
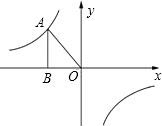 如图所示,已知反比例函数y=$\frac{k}{x}$(k<0)的图象经过点A(-$\sqrt{3}$,m),过点A作AB⊥x轴于点B,且△AOB的面积为2$\sqrt{3}$.
如图所示,已知反比例函数y=$\frac{k}{x}$(k<0)的图象经过点A(-$\sqrt{3}$,m),过点A作AB⊥x轴于点B,且△AOB的面积为2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
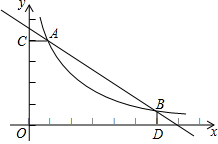 如图,已知点A(1,4),点B(6,$\frac{2}{3}$)是一次函数y=kx+b图象与反比例函数y=$\frac{m}{x}$(m>0)图象的交点,AC⊥y轴于点C,BD⊥x轴于点D.
如图,已知点A(1,4),点B(6,$\frac{2}{3}$)是一次函数y=kx+b图象与反比例函数y=$\frac{m}{x}$(m>0)图象的交点,AC⊥y轴于点C,BD⊥x轴于点D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
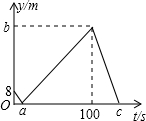 甲、乙两人在一条长为500m的直线跑道上同起点、同向匀速跑步,已知甲先出发2s后乙再出发,先到终点的人原地休息,如图表示的是甲、乙两人之间的距离y(m)与乙出发的时间t(s)的函数关系,给出以下结论:①a=8;②b=92;③c=23,其中正确的是( )
甲、乙两人在一条长为500m的直线跑道上同起点、同向匀速跑步,已知甲先出发2s后乙再出发,先到终点的人原地休息,如图表示的是甲、乙两人之间的距离y(m)与乙出发的时间t(s)的函数关系,给出以下结论:①a=8;②b=92;③c=23,其中正确的是( )| A. | ①②③ | B. | ①② | C. | ①③ | D. | ②③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com