
如图,⊿ACB和⊿ECD都是等腰直角三角形,⊿ACB的顶点A在⊿ECD的斜边DE上,若 ,则
,则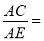 。
。
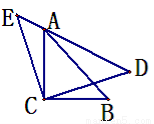
 .
.
【解析】
试题分析:连接BD,可证明AE2+AD2=2AC2,由 可知AD=3AE,代入即可求出
可知AD=3AE,代入即可求出 .
.
试题解析:证明:连结BD,

∵△ACB与△ECD都是等腰直角三角形,
∴∠ECD=∠ACB=90°,∠E=∠ADC=∠CAB=45°,EC=DC,AC=BC,AC2+BC2=AB2,
∴2AC2=AB2.∠ECD-ACD=∠ACB-∠ACD,
∴∠ACE=∠BCD.
在△AEC和△BDC中, ,
,
∴△AEC≌△BDC(SAS).
∴AE=BD,∠E=∠BDC.
∴∠BDC=45°,
∴∠BDC+∠ADC=90°,
即∠ADB=90°.
∴AD2+BD2=AB2,
∴AD2+AE2=2AC2
又
∴AD=3AE
∴9AE2+AE2=2AC2
∴
考点: 1.全等三角形的判定与性质;2.勾股定理;3.等腰直角三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2015届湖北省鄂州市梁子湖区八年级下学期联考数学试卷(解析版) 题型:解答题
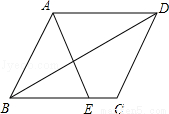
如图,在平行四边形ABCD中,E为BC边上的一点,连结AE、BD且AE=AB.
(1)求证:∠ABE=∠EAD;
(2)若∠AEB=2∠ADB,求证:四边形ABCD是菱形.
查看答案和解析>>
科目:初中数学 来源:2015届湖北省鄂州市梁子湖区八年级下学期联考数学试卷(解析版) 题型:选择题
以下列各组数为边的三角形中,是直角三角形的有( )
(1)3,4,5;(2) ,
,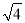 ,
,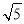 ;(3)32,42,52;(4)0.03,0.04,0.05.
;(3)32,42,52;(4)0.03,0.04,0.05.
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com