
 如图,已知点A,B,C,D在⊙O上,AC⊥BD,垂足为P,OE⊥AB,垂足为E,点F为CD中点,连接OF,PE,PF,试判断四边形OFPE的形状,并说明理由.
如图,已知点A,B,C,D在⊙O上,AC⊥BD,垂足为P,OE⊥AB,垂足为E,点F为CD中点,连接OF,PE,PF,试判断四边形OFPE的形状,并说明理由. 分析 四边形OFPE的形状是平行四边形,连接AO并延长交⊙O于G,连接BG,BC,利用已知条件和圆周角定理可证明BG=DC,进而可证明OE=PF,同理可得PE=OF,继而可得四边形OFPE的形状.
解答 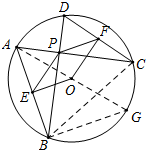 解:四边形OFPE的形状是平行四边形,理由如下:
解:四边形OFPE的形状是平行四边形,理由如下:
∵AG为直径,∴∠ABG=90°,
∴∠ABD+∠DBG=90°且∠BAC+∠ABD=90,
∴∠BAC=∠DBG,
∴$\widehat{BC}$=$\widehat{DG}$,
∴$\widehat{DC}$=$\widehat{BG}$,
∴BG=CD,
∵OE⊥AB,
∴AE=BE,且AO=OG,
∴OE=$\frac{1}{2}$BG=$\frac{1}{2}$CD,
∵RT△PCD,PF为中线,
∴PF=$\frac{1}{2}$CD,
∴OE=PF,
同理可得PE=OF,
∴OFPE为平行四边形.
点评 本题考查了三角形中位线定理,垂径定理以及圆周角定理的运用,题目的综合性较强,添加辅助线较多,解题的关键是熟记并且灵活运用和圆有关的性质定理.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:填空题
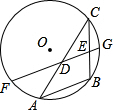 如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点D、E分别是AC、BC的中点,直线DE交⊙O于F、G两点.若⊙O的半径7,则FD+EG的最大值为10.5.
如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点D、E分别是AC、BC的中点,直线DE交⊙O于F、G两点.若⊙O的半径7,则FD+EG的最大值为10.5.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图表示小亮从家出发步行到公交车站,等公交车最后到达学校,图中的折线表示小亮的行程s(km)与所花时间t(min)之间的函数关系,下列说法中正确的个数有( )
如图表示小亮从家出发步行到公交车站,等公交车最后到达学校,图中的折线表示小亮的行程s(km)与所花时间t(min)之间的函数关系,下列说法中正确的个数有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
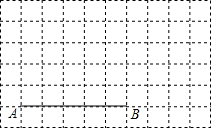 如图,在10×6的正方形网络中,每一个小正方形的边长均为1,线段AB的端点A、B均为在小正方形的顶点上.
如图,在10×6的正方形网络中,每一个小正方形的边长均为1,线段AB的端点A、B均为在小正方形的顶点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 最小值y=$-\frac{1}{2}$ | B. | 最小值y=-1 | C. | 最大值y=$-\frac{1}{2}$ | D. | 最大值y=-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com