
【题目】阅读下列解答过程:(1)如图甲,AB∥CD,探索∠P与∠A,∠C之间的关系.
(2)如图乙和图丙,AB∥CD,请根据上述方法分别探索两图中∠P与∠A,∠C之间的关系.
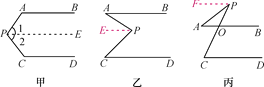
【答案】(1)∠APC+∠A+∠C=360°.(2)∠C-∠A=∠APC
【解析】
(1)过点P作PE∥AB,即可证得 PE∥AB∥CD,根据平行线的性质可得∠1+∠A=180°,∠2+∠C=180°,即可得∠1+∠A+∠2+∠C=360°,再由∠APC=∠1+∠2,即可得∠APC+∠A+∠C=360°;(2)图乙,过P作PE∥AB,求出AB∥PE∥CD,根据平行线的性质得出∠A=∠APE,∠C=∠CPE,即可求出答案;图丙,过点P作PF∥AB,类比图乙的证明方法解答即可.
(1)过点P作PE∥AB.

∵AB∥CD,
∴PE∥AB∥CD(平行于同一条直线的两条直线互相平行).
∴∠1+∠A=180°(两直线平行,同旁内角互补),
∠2+∠C=180°(两直线平行,同旁内角互补).
∴∠1+∠A+∠2+∠C=360°.
又∵∠APC=∠1+∠2,
∴∠APC+∠A+∠C=360°.
(2)如图乙,过点P作PE∥AB.

∵AB∥CD(已知),
∴PE∥AB∥CD(平行于同一直线的两条直线平行).
∴∠A=∠EPA,∠EPC=∠C(两直线平行,内错角相等).
∵∠APC=∠EPA+∠EPC,
∴∠APC=∠A+∠C(等量代换).
如图丙,过点P作PF∥AB.
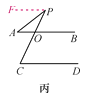
∴∠FPA=∠A(两直线平行,内错角相等).
∵AB∥CD(已知),
∴PF∥CD(平行于同一直线的两条直线平行).
∴∠FPC=∠C(两直线平行,内错角相等).
∵∠FPC-∠FPA=∠APC,
∴∠C-∠A=∠APC(等量代换).


科目:初中数学 来源: 题型:
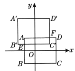
【题目】如图,长方形ABCD各顶点分别为A(-2,2),B(-2,-1),C(3,-1),D(3,2),如果长方A'B'C'D'先向右平移1个单位长度,再向下平移2个单位长度,恰能与长方形ABCD完全重合.
(1)求长方形A'B'C'D'各顶点的坐标;
(2)如果线段AB与线段B'C'交于点E,线段AD与线段C'D'交于点F,求点E,F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平台AB高为12m,在B处测得楼房CD顶部点D的仰角为45°,底部点C的俯角为30°,求楼房CD的高度(结果保留整数,参考值: ![]() ≈1.732)
≈1.732)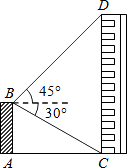
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下两小题后作出相应的解答:
(1)“同位角相等,两直线平行”,“两直线平行,同位角相等”,这两个命题的题设和结论在命题中的位置恰好对凋,我们把其中一命题叫做另一个命题的逆命题,请你写出命题“角平分线上的点到角两边的距离相等“的逆命题,并指出逆命题的题设和结论;
(2)根据以下语句作出图形,并写出该命题的文字叙述.
已知:过直线AB上一点O任作射线OC,OM、ON分别平分∠AOC、∠BOC,则OM⊥ON.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,射线CB∥OA,∠C=∠OAB=100°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF。
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC∶∠OFC的值是否随之变化?若变化,找出变化规律;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
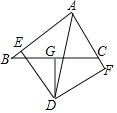
【题目】如图,△ABC中,BC=a,AC=b,AB=c(b<c<a),BC的垂直平分线DG交∠BAC的角平分线AD于点D,DE⊥AB于E,DF⊥AC于F,则下列结论一定成立的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数3.3,-2,0,![]() ,-3.5.
,-3.5.
(1) 比较这些数的大小,并用“<”号连接起来;
(2) 比较这些数的绝对值的大小,并将这些数的绝对值用“>”号连接起来;
(3) 比较这些数的相反数的大小,并将这些数的相反数用“<”号连接起来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB、BC、AC三边的长分别为![]() ,
, ![]() ,
, ![]() ,求这个三角形的面积.小明同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
,求这个三角形的面积.小明同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
(1)△ABC的面积为 .
(2)若△DEF的三边DE、EF、DF长分别为![]() ,
, ![]() ,
, ![]() ,请在图2的正方形网格中画出相应的△DEF,并求出△DEF的面积为 .
,请在图2的正方形网格中画出相应的△DEF,并求出△DEF的面积为 .
(3)在△ABC中,AB=2![]() ,AC=4,BC=2,以AB为边向△ABC外作△ABD(D与C在AB异侧),使△ABD为等腰直角三角形,则线段CD的长为 .
,AC=4,BC=2,以AB为边向△ABC外作△ABD(D与C在AB异侧),使△ABD为等腰直角三角形,则线段CD的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十一”长假期间,小张和小李决定骑自行车外出旅游,两人相约一早从各自家中出发,已知两家相距10千米,小张出发必过小李家.
(1)若两人同时出发,小张车速为20千米,小李车速为15千米,经过多少小时能相遇?
(2)若小李的车速为10千米,小张提前20分钟出发,两人商定小李出发后半小时二人相遇,则小张的车速应为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com