
【题目】如图,抛物线y=﹣x2+(m﹣1)x+m(m>1)与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C(0,3).
(1)求抛物线的解析式;
(2)点D和点C关于抛物线的对称轴对称,点你F在直线AD上方的抛物线上,FG⊥AD于G,FH∥x轴交直线AD于H,求△FGH的周长的最大值;
(3)点M是抛物线的顶点,直线l垂直于直线AM,与坐标轴交于P、Q两点,点R在抛物线的对称轴上,使得△PQR是以PQ为斜边的等腰直角三角形,求直线l的解析式.
【答案】
(1)
解:把C(0,3)代入y=﹣x2+(m﹣1)x+m得m=3,
∴抛物线的解析式为:y=﹣x2+2x+3,
(2)
解:令y=﹣x2+2x+3=0,解得:x1=﹣1,x2=3,∴A(﹣1,0),B(3,0),C(0,3),
∵点D和点C关于抛物线的对称轴对称,
∴D(1,2),AD的解析式y=x+1,
∴OA=OE=1,
∴∠EAO=45°,
∵FH∥AB,
∴∠FHA=∠EAO=45°,
∵FG⊥AH,
∴△FGH是等腰直角三角形,
设点F坐标(m,﹣m2+2m+3),
∴点H坐标(﹣m2+2m+2,﹣m2+2m+3),
∴FH=﹣m2+m+2,
∴△FGH的周长=(﹣m2+m+2)+2× ![]() (﹣m2+m+2)=﹣(1+
(﹣m2+m+2)=﹣(1+ ![]() )(m﹣
)(m﹣ ![]() )2+
)2+ ![]()
∴△FGH的周长最大值为 ![]() ;
;
(3)
解:∵抛物线y=﹣x2+2x+3的定点坐标为(1,4),
∴直线AM的解析式为y=2x+2,
∵直线l垂直于直线AM,
∴设直线l的解析式为y=﹣ ![]() x+b,
x+b,
∵与坐标轴交于P、Q两点,
∴直线l的解析式为y=﹣ ![]() x+b与y轴的交点P(0,b),与x轴的交点Q(2b,0),
x+b与y轴的交点P(0,b),与x轴的交点Q(2b,0),
设R(1,a),
∴PR2=(﹣1)2+(a﹣b)2,QR2=(2b﹣1)2+a2,PQ2=b2+(2b)2=5b2,
∵△PQR是以PQ为斜边的等腰直角三角形,
∴PR2=QR2,即(﹣1)2+(a﹣b)2=QR2=(2b﹣1)2+a2,
∴﹣2a=3b﹣4,①
∴PR2+QR2=PQ2,
即(﹣1)2+(a﹣b)2+(2b﹣1)2+a2=5b2,
∴2a2﹣2ab﹣4b+2=0,②
联立①②解得: ![]() ,
, ![]() ,
,
∴直线l的解析式为y=﹣ ![]() x+
x+ ![]() 或y=﹣
或y=﹣ ![]() x+2.
x+2.
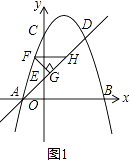
【解析】(1)求出A、D两点坐标,利用待定系数法即可解决问题.(2)首先证明△FHG是等腰直角三角形,构建二次函数利用函数性质解决问题即可;(3)求得直线AM的解析式为y=2x+2,根据直线l垂直于直线AM,设直线l的解析式为y=﹣ ![]() x+b,得到直线l的解析式为y=﹣
x+b,得到直线l的解析式为y=﹣ ![]() x+b与y轴的交点P(0,b),与x轴的交点Q(2b,0),设R(1,a),根据勾股定理列方程即可得到结论.
x+b与y轴的交点P(0,b),与x轴的交点Q(2b,0),设R(1,a),根据勾股定理列方程即可得到结论.
【考点精析】关于本题考查的二次函数的性质,需要了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能得出正确答案.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=ax﹣a(a为常数)的图象与y轴相交于点A,与函数 ![]() 的图象相交于点B(m,1).
的图象相交于点B(m,1). 
(1)求点B的坐标及一次函数的解析式;
(2)若点P在y轴上,且△PAB为直角三角形,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD= ![]() ;正确的是( )
;正确的是( ) 
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA,BC的平行线交于点E,且DE交AC于点O,连接AE. 
(1)求证:四边形ADCE是菱形;
(2)若AC=2DE,求sin∠CDB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A是双曲线 ![]() 在第一象限分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第四象限内,且随着点A的运动,点C的位置也在不断变化,但点C始终在双曲线
在第一象限分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第四象限内,且随着点A的运动,点C的位置也在不断变化,但点C始终在双曲线 ![]() 上运动,则k的值是 .
上运动,则k的值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,AC>BC. 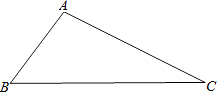
(1)尺规作图:在AC边上求作一点P,使PB=PC(保留作图痕迹,不写作法);
(2)若BC=6,∠C=30°,求△PBC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=60°,AB=12cm,将△ABC以点B为中心顺时针旋转,使点C旋转到AB边延长线上的点D处,则AC边扫过的图形(阴影部分)的面积是cm2 . (结果保留π). 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形OABC的顶点C的坐标为(3,4).顶点A在x轴的正半轴上,反比例函数y= ![]() (x>0)的图象经过顶点B,则k的值为( )
(x>0)的图象经过顶点B,则k的值为( )
A.12
B.20
C.24
D.32
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com