
 如图,在△ABC中,AB=AC,点D在边BC上,根据等腰三角形″三线合一″的性质填写结论:
如图,在△ABC中,AB=AC,点D在边BC上,根据等腰三角形″三线合一″的性质填写结论: 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:解答题
 如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F,BD交AE于M.
如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F,BD交AE于M.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某园艺公司对一块直角三角形的花圃进行改造,测得两直角边长为6m,8m,现要将其扩建成等腰三角形,且扩充部分是以8m为直角边的直角三角形,求扩建后的等腰三角形花圃的周长.
某园艺公司对一块直角三角形的花圃进行改造,测得两直角边长为6m,8m,现要将其扩建成等腰三角形,且扩充部分是以8m为直角边的直角三角形,求扩建后的等腰三角形花圃的周长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
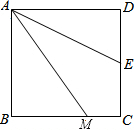 如图,已知四边形ABCD是正方形,M是BC边上一点,E是CD边的中点,AE平分∠DAM.
如图,已知四边形ABCD是正方形,M是BC边上一点,E是CD边的中点,AE平分∠DAM.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com