
ЁОЬтФПЁПЃЈ12ЗжЃЉШчЭМЃЌдкжБНЧзјБъЯЕжаЃЌRtЁїOABЕФжБНЧЖЅЕуAдкxжсЩЯЃЌOA=4ЃЌAB=3ЃЎЖЏЕуMДгЕуAГіЗЂЃЌвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЃЌбиAOЯђжеЕуOвЦЖЏЃЛЭЌЪБЕуNДгЕуOГіЗЂЃЌвдУПУы1ЃЎ25ИіЕЅЮЛГЄЖШЕФЫйЖШЃЌбиOBЯђжеЕуBвЦЖЏЃЎЕБСНИіЖЏЕудЫЖЏСЫxУыЃЈ0ЃМxЃМ4ЃЉЪБЃЌНтД№ЯТСаЮЪЬтЃК
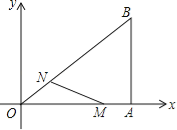
ЃЈ1ЃЉЧѓЕуNЕФзјБъЃЈгУКЌxЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЃЈ2ЃЉЩшЁїOMNЕФУцЛ§ЪЧSЃЌЧѓSгыxжЎМфЕФКЏЪ§БэДяЪНЃЛЕБxЮЊКЮжЕЪБЃЌSгазюДѓжЕЃПзюДѓжЕЪЧЖрЩйЃП
ЃЈ3ЃЉдкСНИіЖЏЕудЫЖЏЙ§ГЬжаЃЌЪЧЗёДцдкФГвЛЪБПЬЃЌЪЙЁїOMNЪЧжБНЧШ§НЧаЮЃПШєДцдкЃЌЧѓГіxЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉЃЈxЃЌ ![]() ЃЉЃЛ
ЃЉЃЛ
ЃЈ2ЃЉЕБx=2ЪБЃЌSгазюДѓжЕЃЌзюДѓжЕЪЧ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉxЕФжЕЪЧ2УыЛђ![]() УыЃЎ
УыЃЎ
ЁОНтЮіЁПЪдЬтЃЈ1ЃЉгЩЙДЙЩЖЈРэЧѓГіOBЃЌзїNPЁЭOAгкPЃЌдђNPЁЮABЃЌЕУГіЁїOPNЁзЁїOABЃЌЕУГіБШР§ЪН![]() ЃЌЧѓГіOPЁЂPNЃЌМДПЩЕУГіЕуNЕФзјБъЃЛ
ЃЌЧѓГіOPЁЂPNЃЌМДПЩЕУГіЕуNЕФзјБъЃЛ
ЃЈ2ЃЉгЩШ§НЧаЮЕФУцЛ§ЙЋЪНЕУГіSЪЧxЕФЖўДЮКЏЪ§ЃЌМДПЩЕУГіSЕФзюДѓжЕЃЛ
ЃЈ3ЃЉЗжСНжжЧщПіЃКЂйШєЁЯOMN=90ЁуЃЌдђMNЁЮABЃЌгЩЦНааЯпЕУГіЁїOMNЁзЁїOABЃЌЕУГіБШР§ЪНЃЌМДПЩЧѓГіxЕФжЕЃЛ
ЂкШєЁЯONM=90ЁуЃЌдђЁЯONM=ЁЯOABЃЌжЄГіЁїOMNЁзЁїOBAЃЌЕУГіБШР§ЪНЃЌЧѓГіxЕФжЕМДПЩЃЎ
ЪдЬтНтЮіЃКНтЃКЃЈ1ЃЉИљОнЬтвтЕУЃКMA=xЃЌON=1ЃЎ25xЃЌ
дкRtЁїOABжаЃЌгЩЙДЙЩЖЈРэЕУЃКOB=![]() =5ЃЌ
=5ЃЌ
зїNPЁЭOAгкPЃЌШчЭМ1ЫљЪОЃК

дђNPЁЮABЃЌ
ЁрЁїOPNЁзЁїOABЃЌ
Ёр![]() ЃЌ
ЃЌ
МД![]() ЃЌ
ЃЌ
НтЕУЃКOP=xЃЌPN= ![]() ЃЌ
ЃЌ
ЁрЕуNЕФзјБъЪЧЃЈxЃЌ ![]() ЃЉЃЛ
ЃЉЃЛ
ЃЈ2ЃЉдкЁїOMNжаЃЌOM=4ЉxЃЌOMБпЩЯЕФИпPN= ![]() ЃЌ
ЃЌ
ЁрS=![]() OMPN=
OMPN=![]() ЃЈ4ЉxЃЉ
ЃЈ4ЉxЃЉ ![]() =Љ
=Љ![]()
![]() +
+![]() xЃЌ
xЃЌ
ЁрSгыxжЎМфЕФКЏЪ§БэДяЪНЮЊS=Љ![]()
![]() +
+![]() xЃЈ0ЃМxЃМ4ЃЉЃЌ
xЃЈ0ЃМxЃМ4ЃЉЃЌ
ХфЗНЕУЃКS=Љ![]()
![]() +
+![]() ЃЌ
ЃЌ
ЁпЉ![]() ЃМ0ЃЌ
ЃМ0ЃЌ
ЁрSгазюДѓжЕЃЌ
ЕБx=2ЪБЃЌSгазюДѓжЕЃЌзюДѓжЕЪЧ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉДцдкФГвЛЪБПЬЃЌЪЙЁїOMNЪЧжБНЧШ§НЧаЮЃЌРэгЩШчЯТЃК
ЗжСНжжЧщПіЃКЂйШєЁЯOMN=90ЁуЃЌШчЭМ2ЫљЪОЃК
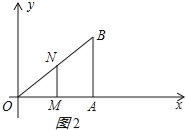
дђMNЁЮABЃЌ
ДЫЪБOM=4ЉxЃЌON=1ЃЎ25xЃЌ
ЁпMNЁЮABЃЌ
ЁрЁїOMNЁзЁїOABЃЌ
Ёр![]() ЃЌ
ЃЌ
МД![]() ЃЌ
ЃЌ
НтЕУЃКx=2ЃЛ
ЂкШєЁЯONM=90ЁуЃЌШчЭМ3ЫљЪОЃК
дђЁЯONM=ЁЯOABЃЌ
ДЫЪБOM=4ЉxЃЌON=1ЃЎ25xЃЌ
ЁпЁЯONM=ЁЯOABЃЌЁЯMON=ЁЯBOAЃЌ
ЁрЁїOMNЁзЁїOBAЃЌ
Ёр![]() ЃЌ
ЃЌ
МД![]() ЃЌ
ЃЌ
НтЕУЃКx=![]() ЃЛ
ЃЛ
злЩЯЫљЪіЃКxЕФжЕЪЧ2УыЛђ![]() УыЃЎ
УыЃЎ




| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЕуAЃЈ1ЃЌaЃЉЪЧЗДБШР§КЏЪ§![]() ЕФЭМЯѓЩЯвЛЕуЃЌжБЯп
ЕФЭМЯѓЩЯвЛЕуЃЌжБЯп![]() гыЗДБШР§КЏЪ§
гыЗДБШР§КЏЪ§![]() ЕФЭМЯѓЕФНЛЕуЮЊЕуBЁЂDЃЌЧвBЃЈ3ЃЌЉ1ЃЉЃЌЧѓЃК
ЕФЭМЯѓЕФНЛЕуЮЊЕуBЁЂDЃЌЧвBЃЈ3ЃЌЉ1ЃЉЃЌЧѓЃК
ЃЈ1ЃЉЧѓЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЧѓЕуDзјБъЃЌВЂжБНгаДГіy1ЃОy2ЪБxЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉЖЏЕуPЃЈxЃЌ0ЃЉдкxжсЕФе§АыжсЩЯдЫЖЏЃЌЕБЯпЖЮPAгыЯпЖЮPBжЎВюДяЕНзюДѓЪБЃЌЧѓЕуPЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКЁїABCдкзјБъЦНУцФкЃЌШ§ИіЖЅЕуЕФзјБъЗжБ№ЮЊAЃЈ0ЃЌ3ЃЉЃЌBЃЈ3ЃЌ4ЃЉЃЌCЃЈ2ЃЌ2ЃЉЃЎЃЈе§ЗНаЮЭјИёжаЃЌУПИіаЁе§ЗНаЮЕФБпГЄЪЧ1ИіЕЅЮЛГЄЖШЃЉЃЎ
ЃЈ1ЃЉзїГіЁїABCШЦЕуAЫГЪБеыЗНЯђа§зЊ90ЁуКѓЕУЕНЕФЁїA1B1C1ЃЌВЂжБНгаДГіC1ЕуЕФзјБъЃЛ
ЃЈ2ЃЉзїГіЁїABCЙигкдЕуOГЩжааФЖдГЦЕФЁїA2B2C2ЃЌВЂжБНгаДГіB2ЕФзјБъЃЎ
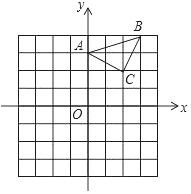
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЦѓвЕЩшМЦСЫвЛПюЙЄвеЦЗЃЌУПМўЕФГЩБОЪЧ50дЊЃЌЮЊСЫКЯРэЖЈМлЃЌЭЖЗХЪаГЁНјааЪдЯњЃЎОнЪаГЁЕїВщЃЌЯњЪлЕЅМлЪЧ100дЊЪБЃЌУПЬьЕФЯњЪлСПЪЧ50МўЃЌЖјЯњЪлЕЅМлУПНЕЕЭ1дЊЃЌУПЬьОЭПЩЖрЪлГі5МўЃЌЕЋвЊЧѓЯњЪлЕЅМлВЛЕУЕЭгкГЩБОЃЎ
ЃЈ1ЃЉЕБЯњЪлЕЅМлЮЊ70дЊЪБЃЌУПЬьЕФЯњЪлРћШѓЪЧЖрЩйЃП
ЃЈ2ЃЉЧѓГіУПЬьЕФЯњЪлРћШѓyЃЈдЊЃЉгыЯњЪлЕЅМлxЃЈдЊЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂЧѓГіздБфСП![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉШчЙћИУЦѓвЕУПЬьЕФзмГЩБОВЛГЌЙ§7000дЊЃЌФЧУДЯњЪлЕЅМлЮЊЖрЩйдЊЪБЃЌУПЬьЕФЯњЪлРћШѓзюДѓЃПзюДѓРћШѓЪЧЖрЩйЃПЃЈУПЬьЕФзмГЩБОЃНУПМўЕФГЩБОЁСУПЬьЕФЯњЪлСПЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁїABCдкЦНУцжБНЧзјБъЯЕжаЕФЮЛжУШчЭМЫљЪОЃЌНЋЁїABCбиyжсЗелЕУЕНЁїA1B1C1ЃЌдйНЋЁїA1B1C1ШЦЕуOа§зЊ180ЁуЕУЕНЁїA2B2C2ЃЛвбжЊAЃЈЉ1ЃЌ4ЃЉЃЌBЃЈЉ2ЃЌ2ЃЉЃЌCЃЈ0ЃЌ1ЃЉ
ЃЈ1ЃЉЧывРДЮЛГіЁїA1B1C1КЭЁїA2B2C2ЃЛ
ЃЈ2ЃЉШєжБЯпA1B2гывЛИіЗДБШР§КЏЪ§ЭМЯѓдкЕквЛЯѓЯоНЛгкЕуA1ЃЌЪдЧѓжБЯпA1B2КЭетИіЗДБШР§КЏЪ§ЕФНтЮіЪНЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬГЁЯњЪлвЛХњУћХЦГФЩРЃЌЦНОљУПЬьПЩЪлГі20МўЃЌУПМўгЎРћ40дЊЃЌЮЊСЫРЉДѓЯњЪлЃЌдіМггЎРћЃЌОЁПьМѕЩйПтДцЃЌЩЬГЁОіЖЈВЩШЁЪЪЕБЕФНЕМлДыЪЉЃЌОЕїВщЗЂЯжЃЌШчЙћУПМўГФЩРУПНЕМл1дЊЃЌЩЬГЁЦНОљУПЬьПЩЖрЪлГі2МўЃЎЧѓЃК
ЃЈ1ЃЉШєЩЬГЁЦНОљУПЬьвЊгЎРћ1200дЊЃЌУПМўГФЩРгІНЕМлЖрЩйдЊЃП
ЃЈ2ЃЉУПМўГФЩРНЕМлЖрЩйдЊЪБЃЌЩЬГЁЦНОљУПЬьгЎРћзюЖрЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌвЛЖЏЕуДгАыОЖЮЊ2ЕФЁбOЩЯЕФA0ЕуГіЗЂЃЌбизХЩфЯпA0OЗНЯђдЫЖЏЕНЁбOЩЯЕФЕуA1ДІЃЌдйЯђзѓбизХгыЩфЯпA1OМаНЧЮЊ60ЁуЕФЗНЯђдЫЖЏЕНЁбOЩЯЕФЕуA2ДІЃЛНгзХгжДгA2ЕуГіЗЂЃЌбизХЩфЯпA2OЗНЯђдЫЖЏЕНЁбOЩЯЕФЕуA3ДІЃЌдйЯђзѓбизХгыЩфЯпA3OМаНЧЮЊ60ЁуЕФЗНЯђдЫЖЏЕНЁбOЩЯЕФЕуA4ДІЃЛA4A0МфЕФОрРыЪЧ_____ЃЛЁАДДЫЙцТЩдЫЖЏЕНЕуA2019ДІЃЌдђЕуA2019гыЕуA0МфЕФОрРыЪЧ_____ЃЎ
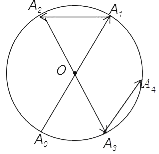
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌСтаЮ ABCD ЕФБп ADЁЮx жсЃЌжБЯпyЃН2x+b гы x жсНЛгкЕу BЃЌгыЗДБШР§КЏЪ§ yЃН![]() ЃЈkЃО0ЃЉЭМЯѓНЛгкЕу D КЭЕу EЃЌOBЃН3ЃЌOAЃН4ЃЎ
ЃЈkЃО0ЃЉЭМЯѓНЛгкЕу D КЭЕу EЃЌOBЃН3ЃЌOAЃН4ЃЎ
ЃЈ1ЃЉЧѓЗДБШР§КЏЪ§КЭвЛДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕу P ЮЊЯпЖЮ BE ЩЯЕФвЛИіЖЏЕуЃЌЙ§Еу P зї x жсЕФЦНааЯпЃЌЕБЁїCDE БЛетЬѕЦНааЯпЗжГЩУцЛ§ЯрЕШЕФСНВПЗжЪБЃЌЧѓЕу P ЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкОиаЮABCDжаЃЌAB=12ЃЌPЪЧБпABЩЯвЛЕуЃЌАбЁїPBCбижБЯпPCелЕўЃЌЖЅЕуBЕФЖдгІЕуЪЧЕуGЃЌЙ§ЕуBзїBEЁЭCGЃЌДЙзуЮЊEЧвдкADЩЯЃЌBEНЛPCгкЕуFЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌШєЕуEЪЧADЕФжаЕуЃЌЧѓжЄЃКЁїAEBЁеЁїDECЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЂйЧѓжЄЃКBP=BFЃЛ
ЂкЕБAD=25ЃЌЧвAEЃМDEЪБЃЌЧѓcosЁЯPCBЕФжЕЃЛ
ЂлЕБBP=9ЪБЃЌЧѓBEEFЕФжЕЃЎ
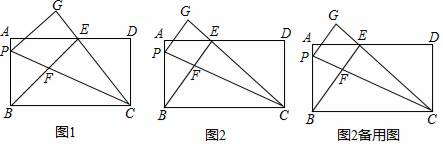
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com