
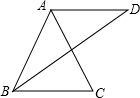
 如图,已知AB=AC=AD,且AD∥BC,试说明∠C与∠D之间的关系.
如图,已知AB=AC=AD,且AD∥BC,试说明∠C与∠D之间的关系. 分析 首先根据AB=AC=AD,可得∠C=∠ABC,∠D=∠ABD,∠ABC=∠CBD+∠D;然后根据AD∥BC,可得∠CBD=∠D,据此判断出∠ABC=2∠D,再根据∠C=∠ABC,即可判断出∠C=2∠D.
解答 解:∠C=2∠D,理由如下:
∵AB=AC=AD,
∴∠C=∠ABC,∠D=∠ABD,
∴∠ABC=∠CBD+∠D,
∵AD∥BC,
∴∠CBD=∠D,
∴∠ABC=∠D+∠D=2∠D,
又∵∠C=∠ABC,
∴∠C=2∠D
点评 (1)此题主要考查了等腰三角形的性质和应用,考查了分类讨论思想的应用,要熟练掌握,解答此题的关键是要明确:①等腰三角形的两腰相等.②等腰三角形的两个底角相等.③等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.
(2)此题还考查了平行线的性质和应用,要熟练掌握,解答此题的关键是要明确:①定理1:两条平行线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角相等.②定理2:两条平行线被地三条直线所截,同旁内角互补.简单说成:两直线平行,同旁内角互补.③定理3:两条平行线被第三条直线所截,内错角相等.简单说成:两直线平行,内错角相等.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:解答题
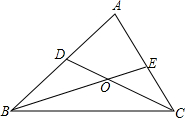 如图所示,在△ABC中,∠ABC和∠ACB的平分线BE和CD相交于点O.
如图所示,在△ABC中,∠ABC和∠ACB的平分线BE和CD相交于点O.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
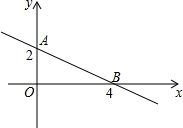 若y=(m-2)${x}^{{m}^{2}-2}$+m-1是一次函数.求:
若y=(m-2)${x}^{{m}^{2}-2}$+m-1是一次函数.求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
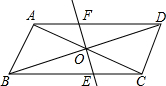 如图,在?ABCD中,AB⊥AC,AB=1,BC=$\sqrt{5}$,对角线AC,BD交于O点,直线EF分别交BC,AD于点E,F
如图,在?ABCD中,AB⊥AC,AB=1,BC=$\sqrt{5}$,对角线AC,BD交于O点,直线EF分别交BC,AD于点E,F查看答案和解析>>
科目:初中数学 来源: 题型:选择题
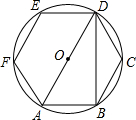 如图所示,正六边形ABCDEF内接于圆O,则cos∠ADB的值为( )
如图所示,正六边形ABCDEF内接于圆O,则cos∠ADB的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
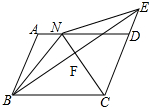 如图,在?ABCD中,∠BCD的平分线CN交?ABCD的边AD于点N,BF⊥CN,交CN于点F,交CD的延长线交于点E,连接BN,NE.若BN=6,BC=8,则△DNE的周长为( )
如图,在?ABCD中,∠BCD的平分线CN交?ABCD的边AD于点N,BF⊥CN,交CN于点F,交CD的延长线交于点E,连接BN,NE.若BN=6,BC=8,则△DNE的周长为( )| A. | 14 | B. | 11 | C. | 9 | D. | 12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com