
【题目】如图,Rt△ABC中,∠ACB=90°,AC=6,AB=10,⊙C与AB相切于点D,延长AC到点E,使CE=AC,连接EB.过点E作BE的垂线,交⊙C于点P、Q,交BA的延长线于点F.
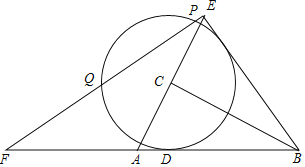
(1)求AD的长;
(2)求证:EB与⊙C相切;
(3)求线段PQ的长.
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]()
【解析】
(1)连结CD,易证△ACD∽△ABC,由相似三角形的性质即可求得AD的长;
(2)过点C作CK⊥BE交BE于点K,要证EB与⊙C相切,即证CK=CD=圆的半径,由∠ACB=90°且CE=AC可证得BE是∠ABE的平分线,即可证得CK=CD;
(3)过点C作CG⊥FE交FE于点G,由矩形的性质和全等三角形的性质得CG=AD,由勾股定理可求得GQ,即可求出PQ.
解:(1)如图,连接CD,
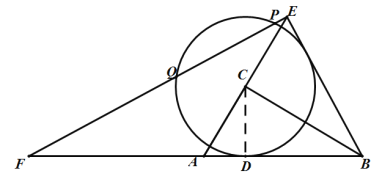
∵⊙C与AB相切于点D,
∴CD⊥AB,则∠ADC=90°,
∴∠CAD+∠ACD=90°,
∵∠ACB=90°,
∴∠CAD+∠CBA=90°,∠ADC=∠ACB=90°,
∴∠ACD=∠CBA,
∴△ACD∽△ABC,
∴![]() ,
,
∵AC=6,AB=10,
∴![]() ,
,
∴AD=![]() ;
;
(2)如图,过点C作CK⊥BE交BE于点K,

∵∠ACB=90°,CE=AC,即BC垂直且平分AE,
∴BA=BE,△BAE是等腰三角形,
∴BC平分∠ABE,
∵CD⊥AB,CK⊥BE,
∴CK=CD=圆的半径,
∴EB与⊙C相切;
(3)如图,过点C作CG⊥FE交FE于点G,连结CQ,
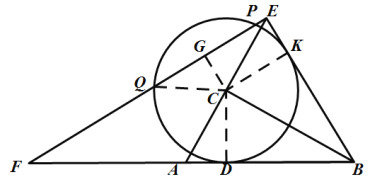
∴PQ=2QG,∠CGE=90°,
又∵EF⊥BE,CK⊥BE,
∴∠GEK=∠CKE=∠CGE=90°,
∴四边形EGCF为矩形,
∴GE=CK,
由(2)可知CK=CD,
∴GE=CD,
在Rt△ADC和Rt△CGE中,
![]()
∴Rt△ADC≌Rt△CGE,
∴CG=AD=![]() ,
,
∵AC=6,AD=![]() ,
,
∴![]() ,
,
∴CQ=CD=![]() ,
,
∴![]() ,
,
∴PQ=2GQ=![]() .
.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
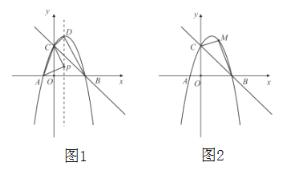
【题目】已知,如图1,抛物线![]() 过
过![]() 三点,顶点为点
三点,顶点为点![]() ,连接
,连接![]() ,点
,点![]() 为抛物线对称轴上一点,连接
为抛物线对称轴上一点,连接![]() ,直线
,直线![]() 过点
过点![]() 两点.
两点.
(1)求抛物线![]() 及直线
及直线![]() 的函数解析式;
的函数解析式;
(2)求![]() 的最小值;
的最小值;
(3)求证:![]() ∽
∽![]() ;
;
(4)如图2,若点![]() 是在抛物线
是在抛物线![]() 上且位于第一象限内的一动点,请直接写出
上且位于第一象限内的一动点,请直接写出![]() 面积的最大值及此时点
面积的最大值及此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标平面内,点O在坐标原点,已知点A(3,1)、B(2,0)、C(4,﹣2).
(1)求证:△AOB∽△OCB;
(2)求∠AOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“安全教育平台”是中国教育学会为方便学长和学生参与安全知识活动、接受安全提醒的一种应用软件.某校为了了解家长和学生参与“防溺水教育”的情况,在本校学生中随机抽取部分学生作调查,把收集的数据分为以下4类情形:A.仅学生自己参与;B.家长和学生一起参与;
C.仅家长自己参与; D.家长和学生都未参与.

请根据图中提供的信息,解答下列问题:
(1)在这次抽样调查中,共调查了________名学生;
(2)补全条形统计图,并在扇形统计图中计算C类所对应扇形的圆心角的度数;
(3)根据抽样调查结果,估计该校2000名学生中“家长和学生都未参与”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于点A(﹣1,0),顶点坐标(1,n),与y轴的交点在(0,3),(0,4)之间(包含端点),则下列结论:①abc>0;②3a+b<0;③﹣
与x轴交于点A(﹣1,0),顶点坐标(1,n),与y轴的交点在(0,3),(0,4)之间(包含端点),则下列结论:①abc>0;②3a+b<0;③﹣![]() ≤a≤﹣1;④a+b≥am2+bm(m为任意实数);⑤一元二次方程
≤a≤﹣1;④a+b≥am2+bm(m为任意实数);⑤一元二次方程![]() 有两个不相等的实数根,其中正确的有( )
有两个不相等的实数根,其中正确的有( )
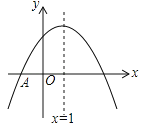
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
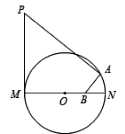
【题目】如图,MN为⊙OD的直径,PM为⊙O的切线,PM=MN=4,点A在⊙O上,AB⊥PA交MN于B.若B为ON的中点,则AB的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
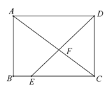
【题目】如图,在矩形 ABCD 中,E 是边 BC 边上一点,连接 DE 交对角线 AC 于点 F,若 AB=6,AD=8,BE=2,则 AF 的长为 _________________ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
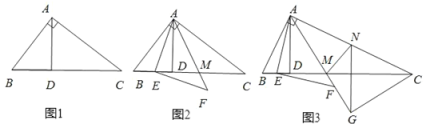
【题目】如图 1,在直角三角形 ABC 中, BAC 90°, AD 为斜边 BC 上的高线.
(1)求证: AD ![]() BD CD ;
BD CD ;
(2)如图 2,过 A 分别作BAD,DAC 的角平分线,交 BC 于 E, M 两点,过 E 作 AE 的垂线, 交 AM 于 F .
①当tan C ![]() 时,求
时,求![]() 的值;
的值;
② 如图 3 ,过 C 作 AF 的垂线 CG ,过 G 点作 GN // AD 交 AC 于 M 点, 连接 MN .若EAD 15°, AB 1,直接写出 MN 的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com