Question

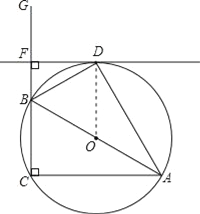
【题目】已知：如图1，∠ACG=90°，AC=2，点B为CG边上的一个动点，连接AB，将△ACB沿AB边所在的直线翻折得到△ADB，过点D作DF⊥CG于点F．

（1）当BC= 时，判断直线FD与以AB为直径的⊙O的位置关系，并加以证明；

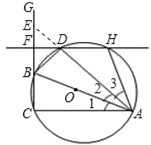
（2）如图2，点B在CG上向点C运动，直线FD与以AB为直径的⊙O交于D、H两点，连接AH，当∠CAB=∠BAD=∠DAH时，求BC的长．

Answer 1

【答案】（1）直线FD与以AB为直径的⊙O相切，理由见解析；（2） .

【解析】试题分析：（1）根据已知及切线的判定证明得，直线FD与以AB为直径的⊙O相切；

（2）根据圆内接四边形的性质及直角三角形的性质进行分析，从而求得BC的长．

试题解析：

（1）判断：直线FD与以AB为直径的⊙O相切．

证明：如图，

作以AB为直径的⊙O；

∵△ADB是将△ACB沿AB边所在的直线翻折得到的，

∴△ADB≌△ACB，

∴∠ADB=∠ACB=90°．

∵O为AB的中点，连接DO，

∴OD=OB=AB，

∴点D在⊙O上．

在Rt△ACB中，BC=，AC=2；

∴tan∠CAB==，

∴∠CAB=∠BAD=30°，

∴∠ABC=∠ABD=60°，

∴△BOD是等边三角形．

∴∠BOD=60°．

∴∠ABC=∠BOD，

∴FC∥DO．

∵DF⊥CG，

∴∠ODF=∠BFD=90°，

∴OD⊥FD，

∴FD为⊙O的切线．

（2）延长AD交CG于点E，

同（1）中的方法，可证点C在⊙O上；

∴四边形ADBC是圆内接四边形．

∴∠FBD=∠1+∠2．

同理∠FDB=∠2+∠3．

∵∠1=∠2=∠3，

∴∠FBD=∠FDB，

又∠DFB=90°．

∴EC=AC=2．

设BC=x，则BD=BC=x，

∵∠EDB=90°，

∴EB=x．

∵EB+BC=EC，

∴x+x=2，

解得x=2﹣2，

∴BC=2﹣2．