
分析 (1)将(7,16)、(5,0)代入y=ax2+bx-75,解方程组即可得;
(2)配方成顶点式即可得最值情况;
(3)根据函数值大于或等于16,可得不等式的解集,可得答案.
解答 解:(1)将点(7,16)、(5,0)代入y=ax2+bx-75,
得:$\left\{\begin{array}{l}{49a+7b-75=16}\\{25a+5b-75=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{b=20}\end{array}\right.$,
故抛物线解析式为:y=-x2+20x-75
(2)y=-x2+20x-75=-(x-10)2+25,
当x=10是,y取得最大值25,
答:销售单价为10元时,该种商品每天的销售利润最大,最大利润为25元;
(2)∵函数y=-x2+20x-75图象的对称轴为直线x=10,
可知点(7,16)关于对称轴的对称点是(13,16),
又∵函数y=-x2+20x-75图象开口向下,
∴当7≤x≤13时,y≥16.
答:销售单价不少于7元且不超过13元时,该种商品每天的销售利润不低于16元.
点评 本题考查了待定系数求二次函数解析式、二次函数的图象与性质,熟练掌握二次函数的图象与性质是关键.


 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中数学 来源: 题型:填空题
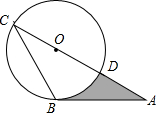 如图,AB是⊙O的切线,B为切点,AC经过点O,与⊙O分别相交于点D,C,若∠ACB=30°,AB=$\sqrt{3}$,则阴影部分的面积是$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$.
如图,AB是⊙O的切线,B为切点,AC经过点O,与⊙O分别相交于点D,C,若∠ACB=30°,AB=$\sqrt{3}$,则阴影部分的面积是$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在扇形ACB中,∠ACB=90°,BC为直径作半圆,圆心为O.过点O作AC的平行线交两弧于点D、E,若BC=2,则阴影部分的面积是$\frac{5}{12}$π-$\frac{\sqrt{3}}{2}$.
如图,在扇形ACB中,∠ACB=90°,BC为直径作半圆,圆心为O.过点O作AC的平行线交两弧于点D、E,若BC=2,则阴影部分的面积是$\frac{5}{12}$π-$\frac{\sqrt{3}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-$\frac{1}{2}$)-2 | B. | -(-$\frac{1}{2}$)0 | C. | (-$\frac{1}{2}$)3 | D. | -|$\frac{1}{2}$| |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
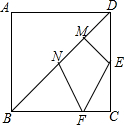 正方形ABCD,AB=4,E是CD中点,BF=3CF,点M,N为线段BD上的动点,MN=$\sqrt{2}$,求四边形EMNF周长的最小值$\sqrt{13}$+$\sqrt{2}$+$\sqrt{5}$.
正方形ABCD,AB=4,E是CD中点,BF=3CF,点M,N为线段BD上的动点,MN=$\sqrt{2}$,求四边形EMNF周长的最小值$\sqrt{13}$+$\sqrt{2}$+$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
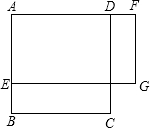 如图,正方形ABCD的边长为5,点E是AB上一点,点F是AD延长线上一点,且BE=DF.四边形AEGF是矩形,则矩形AEGF的面积y与BE的长x之间的函数关系式为( )
如图,正方形ABCD的边长为5,点E是AB上一点,点F是AD延长线上一点,且BE=DF.四边形AEGF是矩形,则矩形AEGF的面积y与BE的长x之间的函数关系式为( )| A. | y=5-x | B. | y=5-x2 | C. | y=25-x | D. | y=25-x2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com