
【题目】股民老黄上星期五买进某股票1000股,每股35元,下表为本周内每日该股票的涨跌情况(单位:元)(注:用正数记股价比前一日上升数,用负数记股价比前一日下降数)
星期 | 一 | 二 | 三 | 四 | 五 |
每股涨跌 | +2.4 | -0.8 | -2.9 | +0.5 | +2.1 |
(1)星期四收盘时,每股是多少元?
(2)本周内最高价每股多少元?最低价每股多少元?
(3)根据交易规则,老黄买进股票时需付0.15%的手续费,卖出时需付成交额0.15%的手续费和0.1%的交易税,如果老黄在星期五收盘前将全部股票卖出,他的收益情况如何?
【答案】
(1)解:依题可得:
星期四收盘时每股是:35+(+2.4)+(-0.8)+(-2.9)+(+0.5)=34.2(元);
答:星期四收盘时每股是34.2元.
(2)解:如图:
∴本周内最高价是每股37.5元,最低价每股33.8元.
答:本周内最高价是每股37.5元,最低价每股33.8元.
(3)解:依题可得:
∴买入总金额 :1000×35=35000 (元);
买入手续费 :35000×0.15%=52.5(元);
卖出总金额 :1000×36.4=36400(元);
卖出手续费 :36400×0.15%=54.6 (元);
卖出交易税:=36400×0.1%=36.4 (元);
∴收益 :36400(35000+52.5+54.6+36.4)
=3640035143.5
=1256.5 (元).
答:他的收益情况是1256.5元.
【解析】(1)根据表格中的数据即可列出代数式即可得出星期四收盘时每股的价格.
(2)根据表格中的数据列出每天收盘时的股价,从而得出本周内最高股价和最低股价.
(3)根据题意分别求出买入总金额、买入手续费、卖出总金额、卖出手续费、卖出交易税,再得出收益的式子,计算即可得出答案.


科目:初中数学 来源: 题型:
【题目】如图所示,点P(3a,a)是反比例函数y= ![]() (k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为( )
(k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为( )
A.y= ![]()
B.y= ![]()
C.y= ![]()
D.y= ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
【发现】
如图∠ACB=∠ADB=90°,那么点D在经过A,B,C三点的圆上(如图①)
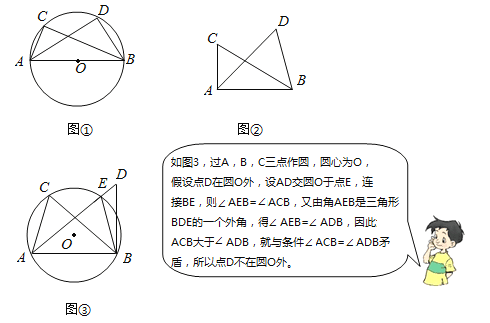
【思考】
如图②,如果∠ACB=∠ADB=a(a≠90°)(点C,D在AB的同侧),那么点D还在经过A,B,C三点的圆上吗?
请证明点D也不在⊙O内.
【应用】
利用【发现】和【思考】中的结论解决问题:若四边形ABCD中,AD∥BC,∠CAD=90°,点E在边AB上,CE⊥DE.
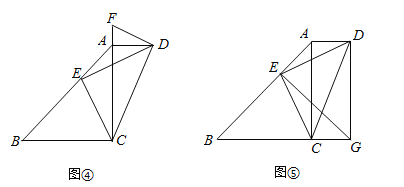
(1)作∠ADF=∠AED,交CA的延长线于点F(如图④),求证:DF为Rt△ACD的外接圆的切线;
(2)如图⑤,点G在BC的延长线上,∠BGE=∠BAC,已知sin∠AED=![]() ,AD=1,求DG的长.
,AD=1,求DG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( ) 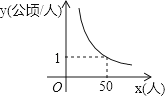
A.该村人均耕地面积随总人口的增多而增多
B.该村人均耕地面积y与总人口x成正比例
C.若该村人均耕地面积为2公顷,则总人口有100人
D.当该村总人口为50人时,人均耕地面积为1公顷
查看答案和解析>>
科目:初中数学 来源: 题型:
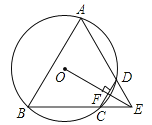
【题目】如图,四边形ABCD是⊙O的内接四边形,BC的延长线与AD的延长线交于点E,且DC=DE.
(1)求证:∠A=∠AEB;
(2)连接OE,交CD于点F,OE⊥CD,求证:△ABE是等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数分别填入相应的集合里.
﹣ 5,﹣2.626 626 662…,0,π,﹣ ![]() ,0.12,|﹣6|.
,0.12,|﹣6|.
(1)正数集合:{}
(2)负数集合:{}
(3)有理数集合:{};
(4)无理数集合:{}.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com