Question

14．如图，△ABC是等腰直角三角形，动点P在斜边AB所在的射线上，以PC为直角边作等腰直角三角形PCQ，已知∠PCQ=90°，设∠ACP=α．
（1）则图中∠BCQ=α（用含α的代数式表示）；
（2）探究：
①由操作知，动点P在射线AB的不同位置时，α的大小不同，直接写出α的取值范围；
②若△PCQ的面积最小，求α的值；
③若△BPC是等腰三角形，求α的值．

Answer 1

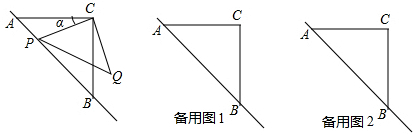
分析 （1）根据同角的余角相等进行判断即可；
（2）①分四种情况讨论：当点P与点A重合时；当点P在AB之间（不与A、B重合）时；当点P与点B重合时；当点P在AB的延长线上时，分别求得α的取值范围；
②根据垂线段最短可得，当CP⊥AB时，CP最短，此时，等腰Rt△PCQ的面积最小，求得α=45°；
③分四种情况讨论，分别根据三角形内角和定理以及等腰直角三角形的性质，求得α的值．

解答 解：（1）∵△ABC是等腰直角三角形，∠PCQ=90°，
∴∠ACB=∠PCQ=90°，
∴∠ACB-∠PCB=∠PCQ-∠PCB，
∴∠ACP=∠BCQ=α，
故答案为：α；

（2）①当点P与点A重合时，∠ACP=α=0°；
当点P在AB之间（不与A、B重合）时，∠ACP为锐角，即0°＜α＜90°；
当点P与点B重合时，∠ACP为直角，即α=90°；
当点P在AB的延长线上时，∠ACP是钝角，90°＜α＜135°；

②根据垂线段最短可得，当CP⊥AB时，CP最短，如图所示，
此时，等腰Rt△PCQ的面积最小，
∴α=∠CPB-∠BAC=90°-45°=45°；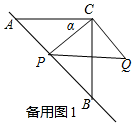


③如图所示，当CA=CB时，△BCP是等腰直角三角形，此时点P与点A重合，∠ACP=α=0°；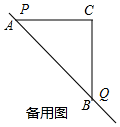

如图所示，当BC=BP时，△BCP是等腰三角形，此时∠BCP=$\frac{180°-45°}{2}$=67.5°，
∴∠ACP=α=90°-67.5°=22.5°；

如图所示，当PB=PC时，△BCP是等腰直角三角形，此时∠PCB=45°，
∴∠ACP=α=90-45°=45°；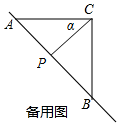

如图所示，当BP=BC时，△BCP是等腰三角形，此时∠BCP=$\frac{45°}{2}$=22.5°，
∴∠ACP=α=90°+22.5°=112.5°；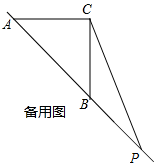

综上所述，α的值为0°，22.5°，45°，112.5°．

点评 本题属于三角形综合题，主要考查了等腰三角形的判定与性质、等腰直角三角形的性质以及三角形内角和定理的综合应用，解决问题的关键是掌握：三角形的内角和等于180°，解题时注意分类讨论思想和垂线段最短的运用，分类时不能重复，也不能遗漏．