Question

【题目】如图，点C在以AB为直径的⊙O上，AD与过点C的切线垂直，垂足为点D，AD交⊙O于点E．

（1） 求证：AC平分∠DAB；

（2） 连接BE交AC于点F，若cos∠CAD＝，求的值．

Answer 1

【答案】（1） 详见解析；（2）.

【解析】试题分析：（1） 连接OC，由已知条件易得∠CAD＝∠OCA，∠OCA＝∠OAC，所以∠CAD＝∠CAO，即可得AC平分∠DAB；（2）．连接BE交OC于点H，易证OC⊥BE，可知∠OCA＝∠CAD，因COS∠HCF＝，可设HC＝4,FC＝5，则FH＝3．由△AEF∽△CHF，设EF＝3x，则AF＝5x，AE＝4x，所以OH＝2x ，在△OBH中，由勾股定理列方程求解即可.

试题解析：（1）证明：连接OC，则OC⊥CD，

又AD⊥CD，

∴AD∥OC，

∴∠CAD＝∠OCA，

又OA＝OC，∴∠OCA＝∠OAC，

∴∠CAD＝∠CAO，

∴AC平分∠DAB．

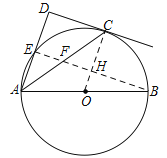
（2）解：连接BE交OC于点H，易证OC⊥BE，可知∠OCA＝∠CAD，

∴COS∠HCF＝，设HC＝4,FC＝5，则FH＝3．

又△AEF∽△CHF，设EF＝3x，则AF＝5x，AE＝4x，∴OH＝2x

∴BH＝HE＝3x＋3 OB＝OC＝2x＋4

在△OBH中，（2x）2＋（3x＋3）2＝（2x＋4）2

化简得：9x2＋2x－7＝0，解得：x＝（另一负值舍去）．

∴．