
【题目】如图,在△ABC中(BC>AC),∠ACB=90°,点D在AB边上,DE⊥AC于点E. 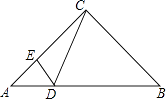
(1)若 ![]() =
= ![]() ,AE=2,求EC的长;
,AE=2,求EC的长;
(2)设点F在线段EC上,点G在射线CB上,以F,C,G为顶点的三角形与△EDC有一个锐角相等,FG交CD于点P.问:线段CP可能是△CFG的高线还是中线?或两者都有可能?请说明理由.
【答案】
(1)解:∵∠ACB=90°,DE⊥AC,
∴DE∥BC,
∴ ![]() ,
,
∵ ![]() ,AE=2,
,AE=2,
∴EC=6
(2)解:①如图1,
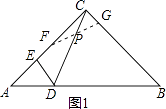
若∠CFG=∠ECD,此时线段CP是△CFG的FG边上的中线.
证明:∵∠CFG+∠CGF=90°,∠ECD+∠PCG=90°,
又∵∠CFG=∠ECD,
∴∠CGF=∠PCG,
∴CP=PG,
∵∠CFG=∠ECD,
∴CP=FP,
∴PF=PG=CP,
∴线段CP是△CFG的FG边上的中线;
②如图2,
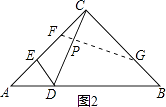
若∠CFG=∠EDC,此时线段CP为△CFG的FG边上的高线.
证明:∵DE⊥AC,
∴∠EDC+∠ECD=90°,
∵∠CFG=∠EDC,
∴∠CFG+∠ECD=90°,
∴∠CPF=90°,
∴线段CP为△CFG的FG边上的高线.
③如图3,
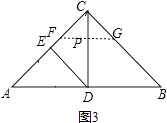
当CD为∠ACB的平分线时,CP既是△CFG的FG边上的高线又是中线.
【解析】(1)易证DE∥BC,由平行线分线段成比例定理列比例式即可求解;(2)分三种情况讨论:①若∠CFG=∠ECD,此时线段CP是△CFG的FG边上的中线;②若∠CFG=∠EDC,此时线段CP为△CFG的FG边上的高线;③当CD为∠ACB的平分线时,CP既是△CFG的FG边上的高线又是中线.
【考点精析】本题主要考查了相似三角形的判定与性质的相关知识点,需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点E在边BC上移动(点E不与点B,C重合),满足∠DEF=∠B,且点D、F分别在边AB、AC上. 
(1)求证:△BDE∽△CEF;
(2)当点E移动到BC的中点时,求证:FE平分∠DFC.
查看答案和解析>>
科目:初中数学 来源: 题型:
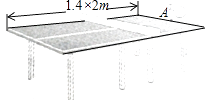
【题目】某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,假设每次发出的乒乓球的运动路线固定不变,且落在中线上.在乒乓球运行时,设乒乓球与端点A的水平距离为x(米),与桌面的高度为y(米),运行时间为t(秒),经多次测试后,得到如下部分数据:
t(秒) | 0 | 0.16 | 0.2 | 0.4 | 0.6 | 0.64 | 0.8 | 6 |
X(米) | 0 | 0.4 | 0.5 | 1 | 1.5 | 1.6 | 2 | … |
y(米) | 0.25 | 0.378 | 0.4 | 0.45 | 0.4 | 0.378 | 0.25 | … |
(1)当t为何值时,乒乓球达到最大高度?
(2)乒乓球落在桌面时,与端点A的水平距离是多少?
(3)乒乓球落在桌面上弹起后,y与x满足y=a(x﹣3)2+k.
①用含a的代数式表示k;
②球网高度为0.14米,球桌长(1.4×2)米.若球弹起后,恰好有唯一的击球点,可以将球沿直线扣杀到点A,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团,要求每位学生都自主选择其中一个社团.为此,随机调查了本校各年级部分学生选择社团的意向,并将调查结果绘制成如下统计图表(不完整):
选择意向 | 所占百分比 |
文学鉴赏 | a |
科学实验 | 35% |
音乐舞蹈 | b |
手工编织 | 10% |
其他 | c |
根据统计图表中的信息,解答下列问题:
(1)求本次调查的学生总人数及a,b,c的值;
(2)将条形统计图补充完整;
(3)若该校共有1200名学生,试估计全校选择“科学实验”社团的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点,设点P(1,t)在反比例函数y= ![]() 的图象上,过点P作直线l与x轴平行,点Q在直线l上,满足QP=OP.若反比例函数y=
的图象上,过点P作直线l与x轴平行,点Q在直线l上,满足QP=OP.若反比例函数y= ![]() 的图象经过点Q,则k= .
的图象经过点Q,则k= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八(1)班五位同学参加学校举办的数学素养竞赛.试卷中共有20道题,规定每题答对得5分,答错扣2分,未答得0分.赛后A,B,C,D,E五位同学对照评分标准回忆并记录了自己的答题情况(E同学只记得有7道题未答),具体如下表
参赛同学 | 答对题数 | 答错题数 | 未答题数 |
A | 19 | 0 | 1 |
B | 17 | 2 | 1 |
C | 15 | 2 | 3 |
D | 17 | 1 | 2 |
E | / | / | 7 |
(1)根据以上信息,求A,B,C,D四位同学成绩的平均分;
(2)最后获知A,B,C,D,E五位同学成绩分别是95分,81分,64分,83分,58分. ①求E同学的答对题数和答错题数;
②经计算,A,B,C,D四位同学实际成绩的平均分是80.75分,与(1)中算得的平均分不相符,发现是其中一位同学记错了自己的答题情况,请指出哪位同学记错了,并写出他的实际答题情况(直接写出答案即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC=4cm,把它沿着对角线AC方向平移1cm得到菱形EFGH,则图中阴影部分图形的面积与四边形EMCN的面积之比为( ) 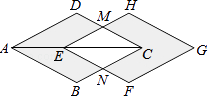
A.4:3
B.3:2
C.14:9
D.17:9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果二次函数的二次项系数为l,则此二次函数可表示为y=x2+px+q,我们称[p,q]为此函数的特征数,如函数y=x2+2x+3的特征数是[2,3].
(1)若一个函数的特征数为[﹣2,1],求此函数图象的顶点坐标.
(2)探究下列问题: ①若一个函数的特征数为[4,﹣1],将此函数的图象先向右平移1个单位,再向上平移1个单位,求得到的图象对应的函数的特征数.
②若一个函数的特征数为[2,3],问此函数的图象经过怎样的平移,才能使得到的图象对应的函数的特征数为[3,4]?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的两条中线AD、CE交于点G,且AD⊥CE,联结BG并延长与AC交于点F,如果AD=9,CE=12,那么下列结论不正确的是( )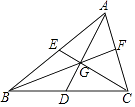
A.AC=10
B.AB=15
C.BG=10
D.BF=15
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com