
(本题满分8分)如图,在 中,
中, ,
,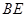 平分
平分 交
交 于点
于点 ,点
,点 在
在 边上且
边上且 .
. 
(1)判断直线 与
与 外接圆的位置关系,并说明理由;
外接圆的位置关系,并说明理由;
(2)若 ,
, ,求
,求 的长.
的长.
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
如图,BC为⊙O的直径,以BC为直角边作Rt△ABC,∠ACB=90°,斜边AB与⊙O交于点D,过点D作⊙O的切线DE交AC于点E,DG⊥BC于点F,交⊙O于点G.
(1)求证:AE=CE;
(2)若AD=4,AE= ,求DG的长.
,求DG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=DB,连结AC,过点D作DE⊥AC于E.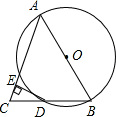
(1)求证:AB=AC;
(2)求证:DE为⊙O的切线;
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级上学期期中调研考试数学试卷(解析版) 题型:解答题
(本题满分10分)如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连结EF、EO,若DE= ,∠DPA=45°.
,∠DPA=45°.

(1)求⊙O的半径;
(2)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级上学期期中调研考试数学试卷(解析版) 题型:选择题
下列事件为必然事件的是( )
A.买一张电影票,座位号是偶数
B.抛掷一枚普通的正方体骰子1点朝上
C.明天一定会下雨
D.百米短跑比赛,一定产生第一名
查看答案和解析>>
科目:初中数学 来源:2014-2015学年黑龙江省伊春市九年级11月月考数学试卷(解析版) 题型:选择题
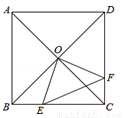
如图,正方形ABCD中,AB=8 cm,对角线AC,BD相交于点O,点E,F分别从B,C两点同 时出发,以1 cm/s的速度沿BC,CD运动,到点C,D时停止运动,设运动时间为t(s),△OEF的面积为S(cm2),则S(cm2)与t(s)的函数关系可用图象表示为( )
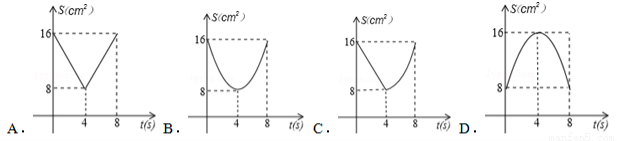
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com