练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】从地面竖直向上抛出一个小球，小球的高度h（米）与运动时间t（秒）之间的关系式为h=30t﹣5t2，那么小球抛出 秒后达到最高点．

    【答案】3

    【解析】

    试题分析：首先理解题意，先把实际问题转化成数学问题后，知道解此题就是求出h=30t﹣5t2的顶点坐标即可．

    解：h=﹣5t2+30t，

    =﹣5（t2﹣6t+9）+45，

    =﹣5（t﹣3）2+45，

    ∵a=﹣5＜0，

    ∴图象的开口向下，有最大值，

    当t=3时，h最大值=45；

    即小球抛出3秒后达到最高点．

    故答案为：3．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在ABCD中，E为BC的中点，连接AE并延长交DC的延长线于点F.

    (1)求证：AB＝CF；

    (2)当BC与AF满足什么数量关系时，四边形ABFC是矩形，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，在四边形ABCD中，AB⊥BC于B点，若AB=3，BC=4，CD=12，AD=13，求四边形ABCD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】定义：我们把三角形被一边中线分成的两个三角形叫做“友好三角形”．

    性质：如果两个三角形是“友好三角形”，那么这两个三角形的面积相等．

    理解：如图①，在△ABC中，CD是AB边上的中线，那么△ACD和△BCD是“友好三角形”，并且S△ACD=S△BCD．

    应用：如图②，在矩形ABCD中，AB=4，BC=6，点E在AD上，点F在BC上，AE=BF，AF与BE交于点O．

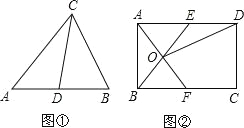
    （1）求证：△AOB和△AOE是“友好三角形”；

    （2）连接OD，若△AOE和△DOE是“友好三角形”，求四边形CDOF的面积．

    探究：在△ABC中，∠A=30°，AB=4，点D在线段AB上，连接CD，△ACD和△BCD是“友好三角形”，将△ACD沿CD所在直线翻折，得到△A′CD，若△A′CD与△ABC重合部分的面积等于△ABC面积的，请直接写出△ABC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】地球平均半径约等于6 400 000米，6 400 000用科学记数法表示为（　　）

    A. 64×105 B. 6.4×105 C. 6.4×106 D. 6.4×107

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】九（1）班数学兴趣小组经过市场调查，整理出某种商品在第x（1≤x≤90）天的售价与销量的相关信息如下表：

    时间x（天）

    1≤x＜50

    50≤x≤90

    售价（元/件）

    x+40

    90

    每天销量（件）

    200-2x

    已知该商品的进价为每件30元，设销售该商品的每天利润为y元．

    （1）求出y与x的函数关系式；

    （2）问销售该商品第几天时，当天销售利润最大，最大利润是多少？

    （3）该商品在销售过程中，共有多少天每天销售利润不低于4800元？请直接写出结果．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若将0.0000065用科学记数法表示为6.5×10n，则n等于（　　）

    A. ﹣5B. ﹣6C. ﹣7D. ﹣8

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某病毒的直径是0.000 068毫米，这个数据用科学记数法表示为_____毫米．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一组数据5，7，10，5，7，5，6，这组数据的众数是

    A. 10B. 7

    C. 6D. 5

    查看答案和解析>>

    同步练习册答案