
【题目】如图,在ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F.
(1)求证:AB=CF;
(2)当BC与AF满足什么数量关系时,四边形ABFC是矩形,并说明理由.

【答案】(1)证明见解析;(2)当BC=AF时,四边形ABFC是矩形.理由见解析.
【解析】试题分析:
(1)利用平行四边形的性质得出∠BAF=∠CFA,进而得出△AEB≌△FEC(AAS),求出答案;
(2)首先得出四边形ABFC是平行四边形,进而得出答案.
试题解析:
(1)证明:∵四边形ABCD是平行四边形,
∴AB∥DF.
∴∠BAF=∠CFA.
∵E为BC的中点,
∴BE=CE.
又∵∠AEB=∠FEC,
∴△AEB≌△FEC(AAS).
∴AB=CF.
(2)当BC=AF时,四边形ABFC是矩形.理由如下:
由(1),得AB=CF,
∵AB∥CF,
∴四边形ABFC是平行四边形.
∵BC=AF,
∴四边形ABFC是矩形.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
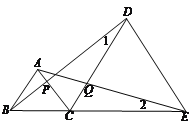
【题目】线段BE上有一点C,以BC,CE为边分别在BE的同侧作等边三角形ABC,DCE,连接AE,BD,分别交CD,CA于Q,P.
(1)找出图中的所有全等三角形.
(2)找出一组相等的线段,并说明理由.
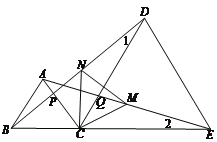
(3)取AE的中点M、BD的中点N,连接MN,试判断三角形CMN的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汉堡店员工小聪去两户家庭外送汉堡和橙汁,第一家送3袋汉堡和2袋橙汁,向顾客收取32元;第二家送2袋汉堡和3袋橙汁,向顾客收取28元.
⑴求汉堡和橙汁的单价;
⑵若某顾客恰好用完36元钱,同时购买汉堡和橙汁,请你帮助小聪设计配送方案;
⑶若某顾客同时购买汉堡和橙汁共10袋,付款不超过55元,问该顾客最多购买汉堡多少袋?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com