Question

【题目】定义：我们把三角形被一边中线分成的两个三角形叫做“友好三角形”．

性质：如果两个三角形是“友好三角形”，那么这两个三角形的面积相等．

理解：如图①，在△ABC中，CD是AB边上的中线，那么△ACD和△BCD是“友好三角形”，并且S△ACD=S△BCD．

应用：如图②，在矩形ABCD中，AB=4，BC=6，点E在AD上，点F在BC上，AE=BF，AF与BE交于点O．

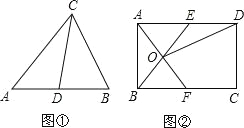
（1）求证：△AOB和△AOE是“友好三角形”；

（2）连接OD，若△AOE和△DOE是“友好三角形”，求四边形CDOF的面积．

探究：在△ABC中，∠A=30°，AB=4，点D在线段AB上，连接CD，△ACD和△BCD是“友好三角形”，将△ACD沿CD所在直线翻折，得到△A′CD，若△A′CD与△ABC重合部分的面积等于△ABC面积的，请直接写出△ABC的面积．

Answer 1

【答案】（1）证明见解析；（2）12.探究：△ABC的面积是2或2．

【解析】

试题分析：（1）利用一组对边平行且相等的四边形是平行四边形，得到四边形ABFE是平行四边形，然后根据平行四边形的性质证得OE=OB，即可证得△AOE和△AOB是友好三角形；

（2）△AOE和△DOE是“友好三角形”，即可得到E是AD的中点，则可以求得△ABE、△ABF的面积，根据S四边形CDOF=S矩形ABCD-2S△ABF即可求解．

探究：画出符合条件的两种情况：①求出四边形A′DCB是平行四边形，求出BC和A′D推出∠ACB=90°，根据三角形面积公式求出即可；②求出高CQ，求出△A′DC的面积．即可求出△ABC的面积．

试题解析：（1）∵四边形ABCD是矩形，

∴AD∥BC，

∵AE=BF，

∴四边形ABFE是平行四边形，

∴OE=OB，

∴△AOE和△AOB是友好三角形．

（2）∵△AOE和△DOE是友好三角形，

∴S△AOE=S△DOE，AE=ED=AD=3，

∵△AOB与△AOE是友好三角形，

∴S△AOB=S△AOE，

∵△AOE≌△FOB，

∴S△AOE=S△FOB，

∴S△AOD=S△ABF，

∴S四边形CDOF=S矩形ABCD-2S△ABF=4×6-2××4×3=12．

探究：

解：分为两种情况：①如图1，

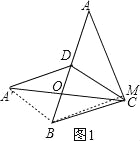
∵S△ACD=S△BCD．

∴AD=BD=AB，

∵沿CD折叠A和A′重合，

∴AD=A′D=AB=×4=2，

∵△A′CD与△ABC重合部分的面积等于△ABC面积的，

∴S△DOC=S△ABC=S△BDC=S△ADC=S△A′DC，

∴DO=OB，A′O=CO，

∴四边形A′DCB是平行四边形，

∴BC=A′D=2，

过B作BM⊥AC于M，

∵AB=4，∠BAC=30°，

∴BM=AB=2=BC，

即C和M重合，

∴∠ACB=90°，

由勾股定理得：AC=，

∴△ABC的面积是×BC×AC=×2×2=2；

②如图2，

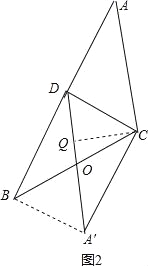
∵S△ACD=S△BCD．

∴AD=BD=AB，

∵沿CD折叠A和A′重合，

∴AD=A′D=AB=×4=2，

∵△A′CD与△ABC重合部分的面积等于△ABC面积的，

∴S△DOC=S△ABC=S△BDC=S△ADC=S△A′DC，

∴DO=OA′，BO=CO，

∴四边形A′BDC是平行四边形，

∴A′C=BD=2，

过C作CQ⊥A′D于Q，

∵A′C=2，∠DA′C=∠BAC=30°，

∴CQ=A′C=1，

∴S△ABC=2S△ADC=2S△A′DC=2××A′D×CQ=2××2×1=2；

即△ABC的面积是2或2．