
����Ŀ���ڵ���ֱ��������ABC�У�AB=AC����BAC=90�㣮��PΪֱ��AB��һ�����㣨��P�����A��B�غϣ�������PC����D��ֱ��BC�ϣ���PD=PC������P��PE^PC����D��E��ֱ��AC��ͬ�࣬��PE=PC������BE��
��1�����һ������P���߶�AB��ʱ��ͼ����ͼ1 ��ʾ��
���������ͼ2������P��BA���ӳ����ϣ���AP��ABʱ���������ⲹȫͼ2����
��2��������⣨1������������У���ѡһ�����������������⣺
����֤����ACP=��DPB��
���õ�ʽ��ʾ�߶�BC��BP��BE֮���������ϵ����֤����
���𰸡�
��1��
�⣺��ȫͼ����ͼ����ʾ

��2��
�⣺���һ��
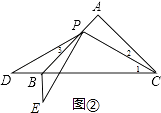
��֤������ͼ�ڣ�
��AB=AC����BAC=90�㣬
���ABC=��ACB=45�㣬
��PD=PC��
���1=��D��
�ߡ�ACB=��1+��2=45�㣬��ABC=��D+��=45�㣬
���3=��2��
����ACP=��DPB��
��BC= ![]() BP+BE�����ɣ�
BP+BE�����ɣ�
֤������ͼ�۹�P��PF��PB��BC��F��
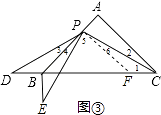
��PF��PB��
���BPF=90�㣬
��EP��PC��
���EPC=90�㣬
���4+��5=��6+��5��
���4=��6��
�ߡ�PBF=45�㣬
���PBF=��PFB=45�㣬
��PB=PF��
�ڡ�PBE���PFC�У�
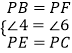 ��
��
���PBE�ա�PFC��
��BE=FC��
��BF= ![]() BP��
BP��
��BC=BF+FC= ![]() BP+BE��
BP+BE��
�����������ͼ�ܣ�
��PD=PC��
���PDC=��PCD��
�ߡ�ABC=��ACB=45�㣬
���3=��PDC��45�㣬��ACP=��PCD��45��
�����BPD=��ACP��
����ͼ�ܣ���P��PF��PB��BC��F��
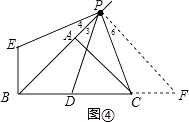
��PF��PB��
���BPF=90�㣬
��EP��PC��
���EPC=90�㣬
���4+��BPC=��6+��BPC=90�㣬
���4=��6��
�ߡ�PBF=45�㣬
���PBF=��PFB=45�㣬
��PB=PF��
�ڡ�PBE���PFC�У�
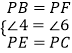 ��
��
���PBE�ա�PFC��
��BE=FC��
��BF= ![]() BP��
BP��
��BC=BF��FC= ![]() BP��BE��
BP��BE��
����������1���������ⲹȫͼ�μ��ɣ���2�����һ���ٸ��ݵ���ֱ�������ε����ʵõ���ABC=��ACB=45�㣬�ɵ��������ε����ʵõ���1=��D���������ε���ǵ����ʼ��ɵõ����ۣ��ڸ�����ǵ����ʵõ���4=��6���ɵ���ֱ�������ε����ʵõ���PBF=��PFB=45�㣬���ǵõ�PB=PF������ȫ�������ε����ʵõ�BE=FC���ɹ��ɶ����õ�BF= ![]() BP�����ɵõ����ۣ�
BP�����ɵõ����ۣ�
��������٣����ݵ��������ε����ʵõ���PDC=��PCD���ɡ�ABC=��ACB=45�㣬���ǵõ���3=��PDC��45�㣬��ACP=��PCD��45�㣬���ɵõ����ۣ�������ǵ����ʵõ���4=��6�����ݵ���ֱ�������ε����ʵõ���PBF=��PFB=45�㣬���ǵõ�PB=PF������ȫ�������ε����ʵõ�BE=FC�����ݹ��ɶ����õ�BF= ![]() BP���ǵõ����ۣ�
BP���ǵõ����ۣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������Ϊ1.6m��С��ABվ�ںӵ�һ�����������ĵ�Ӱȥ���һ����CD�ĸ߶ȣ�CD�ĵ�Ӱ��C��D����AEC����һ�������ϣ��ӿ�BD=12m����BE=2m��������CD=m.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ˮ�����Ű�����ÿ��2Ԫ�ļ۸�ij��ˮ�����ɽȻ����ÿ��4Ԫ�ļ۸���ۣ�ÿ����۳�100�ͨ�����鷢�֣�����ˮ��ÿ����ۼ�ÿ����0.1Ԫ��ÿ��ɶ��۳�20�Ϊ��֤ÿ�������۳�260��Ű��̾����������ۣ�
��1����������ˮ��ÿ����ۼ۽���xԪ����ÿ����������Ƕ��ٽ�ú�x�Ĵ���ʽ��ʾ��
��2����������ˮ��Ҫ��ÿ��ӯ��300Ԫ���Ű����轫ÿ����ۼ۽��Ͷ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪OCƽ����AOB���밴Ҫ��ͼ�����
��1����OC����ȡһ��D������D��OA��OB�Ĵ��߶�DE��DF������ֱ�Ϊ��E��F����֤��OE=OF��
��2������D��OB��ƽ���߽�OA�ڵ�G����֤����ODGΪ���������Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���з��̻����Ӧ���⣺
Ϊף�ر����ɹ����2022�궬�»�����Ȩ��ij����Ʒ���������������춬�»�ɹ��ġ������¡��͡�����ӡ��������һö�������¡���Ҫ�ü���ԭ��4�У�����ԭ��3�У�����һö������ӡ����Ҫ�ü���ԭ��5 �У�����ԭ��10 �У��ó������ס�������ԭ�Ϸֱ�Ϊ20000�к�30000�У������������ԭ������ȫ�������꣬��ô�������������¡��͡�����ӡ��������ö��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���з��̻����Ӧ���⣺
Ϊף�ر����ɹ����2022�궬�»�����Ȩ��ij����Ʒ���������������춬�»�ɹ��ġ������¡��͡�����ӡ��������һö�������¡���Ҫ�ü���ԭ��4�У�����ԭ��3�У�����һö������ӡ����Ҫ�ü���ԭ��5 �У�����ԭ��10 �У��ó������ס�������ԭ�Ϸֱ�Ϊ20000�к�30000�У������������ԭ������ȫ�������꣬��ô�������������¡��͡�����ӡ��������ö��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ xOy�У����ڵ�P��x��y�����Լ������������ͼ��W1��W2 �� ����ͼ��W1��W2�Ϸֱ���ڵ�M ��x1 �� y1 ����N ��x2 �� y2 ����ʹ��P���߶�MN���е㣬��Ƶ�M ��N����P�������������Ƶ�PΪͼ��W1��W2��һ������λ�㡱����ʱP��M��N���������������x= ![]() ��y=
��y= ![]()
��1����֪��A��0��1����B��4��1����C��3����1����D��3����2��������AB��CD��
�ٶ����߶�AB���߶�CD������A��C����P�������������P������Ϊ��
���߶�AB���߶�CD��һ����λ�㡱��Q ��2���� ![]() �������������߶��ϱ���Q��������������������ꣻ
�������������߶��ϱ���Q��������������������ꣻ
��2����ͼ1����֪��R����2��0����������W1��y=x2��2x������������W1�ϵ�ÿһ����M����������W2�϶����ڵ�N��ʹ�õ�N��M ����R��������������ͼ1 �л�������������������W2��
��3��������EFGH�Ķ���ֱ���E����4��1����F����4����1����G����2����1����H����2��1������T��Բ��ΪT��3��0�����뾶Ϊ1������ͼ2�л�����������EFGH�͡�T�����С���λ�㡱��ɵ�ͼ�Σ����漰ƽ����ij������ʱ��������Ӱ��ʾ������ֱ��д����ͼ�ε������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У��Խ���AC �� BD�ཻ�ڵ�O �� ��AC=6cm��BD=8cm������P �� Q�ֱ�ӵ�B �� Dͬʱ�������˶��ٶȾ�Ϊ1cm/s����P��B��C��D�˶�������Dֹͣ����Q��D��O��B�˶�������Oֹͣ1s������˶�������Bֹͣ������AP �� AQ �� PQ �� ���APQ�����Ϊy��cm2��������涨���߶������0�ļ���ͼ�Σ�����P���˶�ʱ��Ϊx��s���� 
��1����գ�AB=cm��AB��CD֮��ľ���Ϊcm��
��2����4��x��10ʱ����y��x֮��ĺ�������ʽ��
��3��ֱ��д���������˶������У�ʹPQ������ABCDһ��ƽ�е�����x��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com