
����Ŀ����֪��![]() ��
��![]() ��
��![]() ��
��![]() �ֱ��ǵ�
�ֱ��ǵ�![]() ��
��![]() ��
��![]() �������϶�Ӧ����.
�������϶�Ӧ����.
��1�����![]() ���
���![]() �ľ��룻
�ľ��룻
��2�����ס�����������ֱ��![]() ��
��![]() ����ͬʱ�������������������˶������ǵ��ٶȷֱ���2��1����λ����/�룩���������ʱ���õ�ʱ�䣻
����ͬʱ�������������������˶������ǵ��ٶȷֱ���2��1����λ����/�룩���������ʱ���õ�ʱ�䣻
��3���ڣ�2���������£������������������˶����Ҷ��������Ḻ�����˶�.�����㿪ʼ�˶�ʱ����������4����λ����/����ٶȺͼ���ͬʱ�ӵ�![]() �������������˶����������������Ҷ���ʱ�������������Ḻ�����˶�������������ʱҲ���Ϸ��أ��������ֱ������������������ֹͣ�˶���������������ڵ�
�������������˶����������������Ҷ���ʱ�������������Ḻ�����˶�������������ʱҲ���Ϸ��أ��������ֱ������������������ֹͣ�˶���������������ڵ�![]() ����������ӿ�ʼ��ֹͣ�˶����������ߵ���·���Լ���
����������ӿ�ʼ��ֹͣ�˶����������ߵ���·���Լ���![]() ��Ӧ������.
��Ӧ������.
���𰸡���1��1����2��������ʱ���õ�ʱ��Ϊ6�룻��3���������˶�����·��Ϊ8����λ���ȣ���D��Ӧ������3.
��������
(1))���þ���ֵ�ķǸ��ԣ����a��b��c��ֵ,�����������뼴�ɣ�
(2)������ס�������������ٶȲ�ٸ���ʱ��=·�̡��ٶȼ��㼴������𰸣�
(3)���������������ʱ����Ҫ��ʱ�䣬��������˶�����·�̣������A�ߵ�·�̣������D��Ӧ��������.
�⣺��1����|a+1|��0����5��b��2��0��|c+2|��0�� |a+1|+��5��b��2+|c+2|��0��
��a+1��0��5��b��0��c+2��0��
��a����1��b��5��c����2��
��AC=��-1��-��-2��=1
��2�������⣬AB=5-��-1��=6
��6�£�2-1��=6
�𣺼�����ʱ���õ�ʱ��Ϊ6��.
��3���������⣬����������ʱ����Ҫ��ʱ��Ϊ
6�£�2+1��=2
��������˶�����·��Ϊ2��4��8����λ���ȣ�
�ߵ�A���ٶ�Ϊ2
���A�ߵ�·��Ϊ2��2=4
���D��Ӧ�����ǣ�-1��+4=3
�𣺱������˶�����·��Ϊ8����λ���ȣ���D��Ӧ������3.


 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
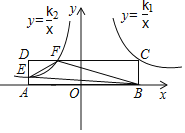
����Ŀ����ͼ������ABCD�Ķ���A��B��x���ϣ��ҹ���y��Գƣ�����������y=![]() ��x��0����ͼ����C������������y=
��x��0����ͼ����C������������y=![]() ��x��0����ͼ��ֱ���AD��CD���ڵ�E��F����S��BEF=7��k1+3k2=0����k1����_____��
��x��0����ͼ��ֱ���AD��CD���ڵ�E��F����S��BEF=7��k1+3k2=0����k1����_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����P���߶�AB�⣬��PA=PB����֤����P���߶�AB�Ĵ�ֱƽ�����ϣ���֤���ý���ʱ�������Ӹ����ߣ�����������ȷ���ǣ�������

A. ����APB��ƽ����PC��AB�ڵ�C
B. ����P��PC��AB�ڵ�C��AC=BC
C. ȡAB�е�C������PC
D. ����P��PC��AB������ΪC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����֪AB=AC��DΪ��BAC�Ľ�ƽ��������һ�㣬����BD��CD����ͼ2����֪AB=AC��D��EΪ��BAC�Ľ�ƽ�����������㣬����BD��CD��BE��CE����ͼ3����֪AB=AC��D��E��FΪ��BAC�Ľ�ƽ�����������㣬����BD��CD��BE��CE��BF��CF���������ι��ɣ���n��ͼ������ȫ�������εĶ�����_________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1��������![]() ��
��![]() ��
��![]() �������ϵĶ�Ӧ����ͼ��ʾ���������ʽ��
�������ϵĶ�Ӧ����ͼ��ʾ���������ʽ��![]()
![]()
��2������ij����������һ�ܴ���������������Ϊ210�֣��ƻ�ÿ�촦��30�֣����ڸ���ԭ��ʵ��ÿ�촦������ƻ�����г��룬ij�������ʵ�ʴ��������¼���£�
+6��-3��+4��-1��+2��-5��0
����������һ��ʵ�ʴ������������Ƕ��ٶ֣�
������������ʵ�м������ʣ�ÿ����һ������������300Ԫ��ͬʱ�ֹ涨�����һ���������⽱100Ԫ���겻��������ٴ���һ�������100Ԫ����ô�ó�������һ�ܵĹ����ܶ��Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
�У�![]() ���ף�
���ף�![]() ��
��![]() ���ף���
���ף���![]() Ϊ
Ϊ![]() ���е㣬�����
���е㣬�����![]() ���߶�
���߶�![]() ����
����![]() ����/����ٶ��ɵ�����˶���ͬʱ��
����/����ٶ��ɵ�����˶���ͬʱ��![]() ���߶�
���߶�![]() ����
����![]() ����
����![]() ���˶�.��һ����ֹͣ�˶�ʱ����һ����Ҳ��ֹ֮ͣ�˶�.
���˶�.��һ����ֹͣ�˶�ʱ����һ����Ҳ��ֹ֮ͣ�˶�.

(1)�ú���![]() �Ĵ���ʽ��ʾ
�Ĵ���ʽ��ʾ![]() ����
����![]() _______���ף�
_______���ף�
(2)����![]() ���˶��ٶ����
���˶��ٶ����![]() ���˶��ٶ���ȣ�����
���˶��ٶ���ȣ�����![]() ���
���![]() ��
��![]() �Ƿ�ȫ�ȣ���˵�����ɣ�
�Ƿ�ȫ�ȣ���˵�����ɣ�
(3)����![]() ���˶��ٶ����
���˶��ٶ����![]() ���˶��ٶȲ���ȣ���ô����
���˶��ٶȲ���ȣ���ô����![]() ���˶��ٶ�Ϊ����ʱ���ܹ�ʹ
���˶��ٶ�Ϊ����ʱ���ܹ�ʹ![]() ��
��![]() ȫ�ȣ�
ȫ�ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
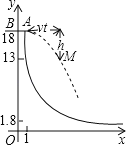
����Ŀ����ͼ���ֻ����صĽ���ʾ��ͼ��ƽ̨AB��x�ᣨˮƽ��18�ף���y�ύ�ڵ�B���뻬��y=![]() ��x��1�����ڵ�A����AB=1�ף��˶�Ա�����ɵ㣩��BA�������ٶ�v��/���A�������·�������M������·�ߵ�ijλ�ã����Կ���������ʵ�������M��A����ֱ����h���ף���ɳ�ʱ��t���룩��ƽ�������ȣ���t=1ʱh=5��M��A��ˮƽ������vt�ף�
��x��1�����ڵ�A����AB=1�ף��˶�Ա�����ɵ㣩��BA�������ٶ�v��/���A�������·�������M������·�ߵ�ijλ�ã����Կ���������ʵ�������M��A����ֱ����h���ף���ɳ�ʱ��t���룩��ƽ�������ȣ���t=1ʱh=5��M��A��ˮƽ������vt�ף�
��1����k������t��ʾh��
��2����v=5����t��ʾ��M�ĺ�����x��������y������y��x�Ĺ�ϵʽ����дx��ȡֵ��Χ������y=13ʱ�˶�Ա�����·���������ֱ���룻
��3�����˶�Ա�ס���ͬʱ��A���ɳ����ٶȷֱ���5��/�롢v����/�룮����x��1.8�ף�����λ�ڼ��Ҳ೬��4.5��λ��ʱ��ֱ��д��t��ֵ��v���ķ�Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������������ҹ��Ŵ���ѧ�ľ���������������һ�����⣺�����лƽ��ö������һʮһö����֮���ʵȣ�������һ������ʮ�������ʽ���һö���ؼ��Σ�����˼�ǣ��״���װ�лƽ�9ö��ÿö�ƽ�������ͬ�����Ҵ���װ�а���11ö��ÿö����������ͬ��������������ȣ��������ཻ��1ö�״����Ҵ�����16���������������Բ��ƣ����ʻƽ𡢰���ÿö���ض�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��CD���Ե�AΪԲ�ģ�С��AC��Ϊ�뾶��Բ�����ֱ�AB��AC��E��F���㣬�ٷֱ���E��FΪԲ�ģ�����![]() EF��Ϊ�뾶��Բ��������Բ�����ڵ�P��������AP����CD�ڵ�M��
EF��Ϊ�뾶��Բ��������Բ�����ڵ�P��������AP����CD�ڵ�M��

��1������ACD=114�㣬���MAB�Ķ�����
��2����CN��AM������ΪN����֤����ACN�ա�MCN��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com