
���� ��1����ϵʽΪ��35��A�������+25��B���������1530��15��A�������+35��B���������1150�������г�����ʽ����⼴�ɣ�
��2���˷�=6000��A�������+8000��B�����������ϣ�1���е��Ա�����ȡֵ��⣮
��� �⣺��1����A������x�ڣ���ô
$\left\{\begin{array}{l}{35x+25��50-x����1530}\\{15x+35��50-x����1150}\end{array}\right.$��
���28��x��30��
����3�ַ�����
����һ��A����28�ڣ�B����12�ڣ�
��������A����29�ڣ�B����11�ڣ�
��������A����30�ڣ�B����10�ڣ�
��2�����˷�Ϊ��6000x+8000����50-x��=-2000x+400000
����һ�κ����������Եó�xԽ��������ԽС��
�ʵ�A������30��ʱ�����˷����٣�����Ϊ340000Ԫ��
�𣺵�A������30�ڣ�B����10��ʱ�����˷���ʡ�������˷�Ϊ340000Ԫ��
���� ������һԪһ�β���ʽ���Ӧ�ã��������Ĺؼ��Ƕ������⣬�ҵ���������IJ��ȹ�ϵʽ�����������ĵ�����ϵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
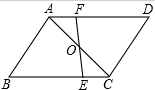 ��ͼ����?ABCD�У�O�ǶԽ���AC���е㣬����O��ֱ��EF�ֱ�BC��AD�ڵ�E��F��֤����
��ͼ����?ABCD�У�O�ǶԽ���AC���е㣬����O��ֱ��EF�ֱ�BC��AD�ڵ�E��F��֤�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2$\sqrt{5}$ | B�� | 5$\sqrt{2}$ | C�� | 10$\sqrt{5}$ | D�� | 5$\sqrt{10}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y��x���������С | B�� | ֱ�߾�����һ������������ | ||
| C�� | ��x��0ʱy��5 | D�� | ֱ����x�ύ�������ǣ�0��5�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com