
【题目】如图,在Rt△ABC中,∠C=90°,O为AB边上一点,⊙O交AB于点E,F两点,BC切⊙O于点D,且CD=![]() EF=1,
EF=1,
(1)求证:AC与⊙O相切;
(2)求图中阴影部分的面积.
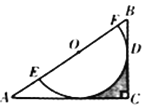
【答案】(1)见解析;(2)1﹣![]() π.
π.
【解析】试题分析:
(1)连接OD,过点O作OH⊥AC于点H,易证四边形ODCH是矩形,由此可得OH=CD=![]() EF=OE,从而可得AC是⊙O的切线;
EF=OE,从而可得AC是⊙O的切线;
(2)由(1)可知∠DOH=90°,OH=![]() EF=1,由此根据:S阴影=S正方形ODCH-S扇形ODH即可计算出阴影部分的面积.
EF=1,由此根据:S阴影=S正方形ODCH-S扇形ODH即可计算出阴影部分的面积.
试题解析:
(1)连接OD,过点O作OH⊥AC于点H,
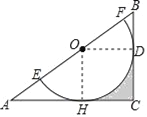
∵BC是⊙O的切线,
∴OD⊥BC.
∵∠C=90°,
∴∠OHC=∠ODC=∠C=90°,
∴四边形OHCD是矩形.
∵CD=![]() EF,
EF,
∴OH=![]() EF=OE.
EF=OE.
∵OH⊥AC,
∴AC是⊙O的切线;
(2)由(1)可知,四边形ODCH是正方形,
∴∠DOH=90°,OH=CD=![]() EF=1,
EF=1,
∴S阴影=S正方形ODCH-S扇形ODH=1×1﹣![]() =1﹣
=1﹣![]() π.
π.



科目:初中数学 来源: 题型:
【题目】某公司销售部有营销人员15人,销售部为了制定某种商品的月销售定额,统计了这15人某月的销售如下:
每人销售件数 | 1800 | 510 | 250 | 210 | 150 | 120 |
人数 | 1 | 1 | 3 | 5 | 3 | 2 |
(1)求这15位营销人员该月销售量的平均数、中位数和众数.
(2)假设销售部负责人把每位营销员的月销售额定为320件,你认为是否合理?为什么?如不合理,请你制定一个合理的销售定额,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的面积为16cm2,△AEF为等腰直角三角形,∠E=90°,AE和BC交于点G,AF和CD交于点H,则△CGH的周长( )

A. 4cmB. 6cmC. 8cmD. 10cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,反比例函数y=![]() (x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点,△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )
(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点,△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )

A. 6![]() B. 10 C. 2
B. 10 C. 2![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
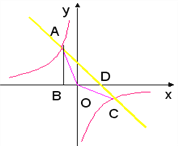
【题目】点A是双曲线![]() 与直线
与直线![]() 在第二象限的交点,AB垂直
在第二象限的交点,AB垂直![]() 轴于点B,且S△ABO=
轴于点B,且S△ABO=![]() .
.
(1)求两个函数的表达式;
(2)求直线与双曲线的交点坐标和△AOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行研学旅行活动,车上准备了7箱矿泉水,每箱的瓶数相同,到达目的地后,先从车上搬下3箱,发给每位同学1瓶矿泉水,有9位同学未领到.接着又从车上搬下4箱,继续分发,最后每位同学都有2瓶矿泉水,还剩下6瓶.问:有多少人参加此次研学旅行活动?每箱矿泉水有多少瓶?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)判断OE与OF的大小关系?并说明理由?
(2)当点O运动何处时,四边形AECF是矩形?并说出你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有5个黄球、13个黑球和22个红球,这些球除颜色外其他都相同.
(1)求从袋中摸出一个球是黄球的概率;
(2)求从袋中摸出一个球不是红球的概率;
(3)现在从袋中取出若干个黑球,并放入相同数量的黄球,搅拌均匀后,若从袋中摸出一个球是黄球的概率为![]() ,则取出了多少个黑球?
,则取出了多少个黑球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个平面直角坐标系.
(1)请在图中描出以下6个点:A(0,2)、B(4,2)、C(3,4)A′(-4,-4)、B'(0,-4)、C′(-1,-2)
(2)分别顺次连接A、B、C和A′、B'、C',得到三角形ABC和三角形A′B′C′;
(3)观察所画的图形,判断三角形A′B′C′能否由三角形ABC平移得到,如果能,请说出三角形A′B′C′是由三角形ABC怎样平移得到的;如果不能,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com