
分析 (1)根据分式的化简方法可以解答本题;
(2)先化简题目中的式子,然后根据题目中的已知式子求出所求式子的值,本题得以解决.
解答 解:(1)-x+$\frac{{x}^{2}}{x-2}$-2
=-(x+2)+$\frac{{x}^{2}}{x-2}$
=$\frac{-(x+2)(x-2)+{x}^{2}}{x-2}$
=$\frac{-{x}^{2}+4+{x}^{2}}{x-2}$
=$\frac{4}{x-2}$;
(2)$\frac{x}{y}$-$\frac{y}{x}$-$\frac{{x}^{2}+{y}^{2}}{xy}$
=$\frac{{x}^{2}-{y}^{2}}{xy}-\frac{{x}^{2}+{y}^{2}}{xy}$
=$-\frac{2y}{x}$,
∵3x2+xy-2y2=0(x≠0,y≠0),
∴3+$\frac{y}{x}-2×\frac{{y}^{2}}{{x}^{2}}=0$,
解得,$\frac{y}{x}$=$\frac{3}{2}$或$\frac{y}{x}=-1$,
∴$-\frac{2y}{x}$=-3或$-\frac{2y}{x}$=2,
即$\frac{x}{y}$-$\frac{y}{x}$-$\frac{{x}^{2}+{y}^{2}}{xy}$的值是-3或2.
点评 本题考查分式的化简求值,解题的关键是明确分式化简求值的方法.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
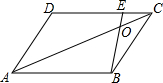 如图平行四边形ABCD中,E为DC上一点,且CE=3,AB=9,对角线AC与BE相交于点O,则S△EOC:S△ABC为( )
如图平行四边形ABCD中,E为DC上一点,且CE=3,AB=9,对角线AC与BE相交于点O,则S△EOC:S△ABC为( )| A. | 1:6 | B. | 1:9 | C. | 1:13 | D. | 1:12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com