
分析 根据题意利用反证法假设$\root{3}{2}$是有理数,进而利用假设得出矛盾,从而得出假设不成立原命题正确.
解答 解:假设$\root{3}{2}$是有理数,
则存在两个互质的正整数m,n,使得$\root{3}{2}$=$\frac{n}{m}$,
于是有2m3=n3,
∵n3是2的倍数,
∴n是2的倍数,
设n=2t(t是正整数),则n3=8t3,即8t3=2m3,
∴4t3=m3,
∴m也是2的倍数,
∴m,n都是2的倍数,不互质,与假设矛盾,
∴假设错误,
∴$\root{3}{2}$不是有理数.
点评 此题主要考查了实数的概念以及反证法的应用,正确掌握反证法的基本步骤是解题关键.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
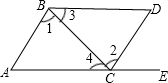 如下图所示,点E在AC的延长线上,下列条件中不能判断BD∥AC( )
如下图所示,点E在AC的延长线上,下列条件中不能判断BD∥AC( )| A. | ∠3=∠4 | B. | ∠1=∠2 | C. | ∠D=∠DCE | D. | ∠D+∠ACD=180° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
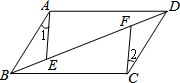 如图,平行四边形ABCD中,E,F是对角线BD上的两点,如果添加一个条件使AE∥CF,则添加的条件不能是( )
如图,平行四边形ABCD中,E,F是对角线BD上的两点,如果添加一个条件使AE∥CF,则添加的条件不能是( )| A. | BF=DE | B. | BE=FD | C. | AE=CF | D. | ∠1=∠2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
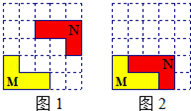 在5×5方格纸中将图①中的图形N平移后的位置如图②所示,那么下面平移中正确的是( )
在5×5方格纸中将图①中的图形N平移后的位置如图②所示,那么下面平移中正确的是( )| A. | 先向下移动1格,再向左移动1格 | B. | 先向下移动1格,再向左移动2格 | ||
| C. | 先向下移动2格,再向左移动1格 | D. | 先向下移动2格,再向左移动2格 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
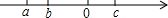 实数a,b,c在数轴上的位置如图所示,则化简$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$+$\sqrt{{c}^{2}}$-$\sqrt{{(a-c)}^{2}}$-$\sqrt{{(b+c)}^{2}}$的结果为( )
实数a,b,c在数轴上的位置如图所示,则化简$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$+$\sqrt{{c}^{2}}$-$\sqrt{{(a-c)}^{2}}$-$\sqrt{{(b+c)}^{2}}$的结果为( )| A. | a-2b | B. | 2b+c | C. | -2a+c | D. | a-2b+c |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com