
【题目】如图,抛物线y=ax2+bx(a≠0) 交x轴正半轴于点A,直线y=2x 经过抛物线的顶点M.已知该抛物线的对称轴为直线x=2,交x轴于点B.
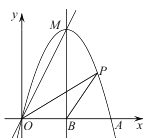
(1)求a,b的值;
(2)P是第一象限内抛物线上的一点,且在对称轴的右侧,连接OP,BP.设点P的横坐标为m ,△OBP的面积为S,![]() .求K关于m 的函数表达式及K的范围.
.求K关于m 的函数表达式及K的范围.
【答案】(1)a=-1;b=4;(2)K=-m+4,0<K<2
【解析】
分析: (1)将x=2代入直线y=2x得出对应的函数值,从而得出M点的坐标,将M点的坐标代入抛物线 y = a x 2 + b x ,再根据抛物线的对称轴为直线 x = 2,得出关于a,b的二元一次方程组,求解得出a,b的值;
(2)如图,过点P作PH⊥x轴于点H,根据P点的横坐标及点P在抛物线上从而得出PH的值,根据B点的坐标得出OB的长,从而根据三角形的面积公式得出S=-m2+4m,再根据![]() ,得出k=-m+4,由题意得A(4,0),M(2,4),根据P是第一象限内抛物线上的一点,且在对称轴的右侧,从而得出2<m<4,根据一次函数的性质知K随着m的增大而减小,从而得出答案0<K<2.
,得出k=-m+4,由题意得A(4,0),M(2,4),根据P是第一象限内抛物线上的一点,且在对称轴的右侧,从而得出2<m<4,根据一次函数的性质知K随着m的增大而减小,从而得出答案0<K<2.
详解:
(1)解 ;将x=2代入y=2x得y=4
∴M(2,4)
由题意得 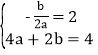 ,
,
∴ ![]() .
.
(2)解 :如图,过点P作PH⊥x轴于点H
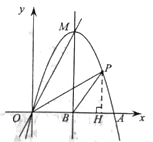
∵点P的横坐标为m,抛物线的函数表达式为y=-x2+4x
∴PH=-m2+4m
∵B(2,0),
∴OB=2
∴S= ![]() OB·PH=
OB·PH=![]() ×2×(-m2+4m)=-m2+4m
×2×(-m2+4m)=-m2+4m
∴K=![]() =-m+4
=-m+4
由题意得A(4,0)
∵M(2,4)
∴2<m<4
∵K随着m的增大而减小,所以0<K<2


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知数轴上A、B两点所表示的数分别为-2和8.
(1)求线段AB的长;
(2)若P为射线BA上的一点(点P不与A、B两点重合,M为PA的中点,N为PB的中点,当点P在射线BA上运动时;MN的长度是否发生改变?若不变,请你画出图形,并求出线段MN的长;若改变,请说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)一个不透明的盒子中装有 2 枚黑色的棋子和 1 枚白色的棋子,每枚棋子除了颜色外其余均相同.从盒中随机摸出一枚棋子,记下颜色后放回并搅匀,再从盒子中随机摸出一枚棋子,记下颜色,用画树状图(或列表)的方法,求两次摸出的棋子颜色不同的概率.
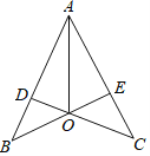
(2)如图,已知 ![]() ,
,![]() ,
,![]() ,
,![]() 交
交![]() 于点O,连接
于点O,连接![]() ,求证:AO平分
,求证:AO平分![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
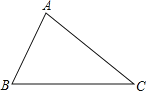
【题目】按要求画图,并解答问题
(1)如图,取BC边的中点D,画射线AD;
(2)分别过点B、C画BE⊥AD于点E,CF⊥AD于点F;
(3)BE和CF的位置关系是 ;通过度量猜想BE和CF的数量关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知P为锐角∠MAN内部一点,过点P作PB⊥AM于点B,PC⊥AN于点C,以PB为直径作⊙O,交直线CP于点D,连接AP,BD,AP交⊙O于点E.

(1)求证:∠BPD=∠BAC.
(2)连接EB,ED,当tan∠MAN=2,AB=2![]() 时,在点P的整个运动过程中.
时,在点P的整个运动过程中.
①若∠BDE=45°,求PD的长;
②若△BED为等腰三角形,求所有满足条件的BD的长;
(3)连接OC,EC,OC交AP于点F,当tan∠MAN=1,OC//BE时,记△OFP的面积为S1,△CFE的面积为S2,请写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
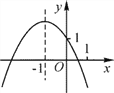
【题目】已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①a+b+c>0;②a-b+c>1;③abc>0;④4a-2b+c<1;⑤b+2a=0. 其中所有正确的结论是______.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:某段楼梯共有10个台阶,如果某同学在上台阶时,可以一步1个台阶,也可以一步2个台阶.那么该同学从该段楼梯底部上到顶部共有多少种不同的走法?
问题探究:
为解决上述实际问题,我们先建立如下数学模型:
如图①,用若干个边长都为1的正方形(记为1×1矩形)和若干个边长分别为1和2的矩形(记为1×2矩形),要拼成一个如图②中边长分别为1和n的矩形(记为1×![]() 矩形),有多少种不同的拼法?(设
矩形),有多少种不同的拼法?(设![]() 表示不同拼法的个数)
表示不同拼法的个数)
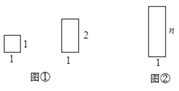
为解决上述数学模型问题,我们采取的策略和方法是:一般问题特殊化.
探究一:先从最特殊的情形入手,即要拼成一个1×1矩形,有多少种不同拼法?
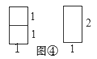
显然,只有1种拼法,如图③,即![]() =1种.
=1种.
探究二:要拼成一个1×2矩形,有多少种不同拼法?
可以看出,有2种拼法,如图④,即![]() =2种.
=2种.
探究三:要拼成一个1×3矩形,有多少种不同拼法?
拼图方法可分为两类:一类是在图④这2种1×2矩形上方,各拼上一个1×1矩形,即这类拼法共有![]() =2种;另一类是在图③这1种1×1矩形上方拼上一个1×2矩形,即这类拼法有
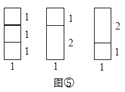
=2种;另一类是在图③这1种1×1矩形上方拼上一个1×2矩形,即这类拼法有![]() =1种.如图⑤,即
=1种.如图⑤,即![]() =
=![]() +
+![]() = 2+1=3(种).
= 2+1=3(种).
![]()
探究四:仿照上述探究过程,要拼成一个1×4矩形,有多少种不同拼法?请画示意图说明并求出结果.
探究五:要拼成一个1×5矩形,仿照上述探究过程,得出![]() = 种不同拼法.
= 种不同拼法.
(直接写出结果,不需画图).
问题解决:请你根据上述中的数学模型,解答“问题提出”中的实际问题.
(写出解答过程,不需画图).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com