
【题目】如图所示,折叠长方形(四个角都是直角)的一边AD使点D落在BC边的点F处,已知AB=DC=8cm,AD=BC=10cm,求EC的长.

【答案】EC的长为3cm.
【解析】
想求得EC长,利用勾股定理计算,需求得FC长,那么就需求出BF的长,利用勾股定理即可求得BF长.
设EC的长为xcm,则DE=(8﹣x)cm,
∵△ADE折叠后的图形是△AFE,
∴AD=AF,∠D=∠AFE,DE=EF,
∵AD=BC=10cm,
∴AF=AD=10cm,
又∵AB=8cm,
在Rt△ABF中,根据勾股定理,得AB2+BF2=AF2,
∴82+BF2=102,
∴BF=6cm,
∴FC=BC﹣BF=10﹣6=4cm,
在Rt△EFC中,根据勾股定理,得:FC2+EC2=EF2,
∴42+x2=(8﹣x)2
即16+x2=64﹣16x+x2,
化简,得16x=48,
∴x=3,
故EC的长为3cm.


科目:初中数学 来源: 题型:
【题目】如图,Rt△AOB的顶点O与原点重合,直角顶点A在x轴上,顶点B的坐标为(4,3),直线![]() 与x轴、y轴分别交于点D、E,交OB于点F.
与x轴、y轴分别交于点D、E,交OB于点F.
(1)写出图中的全等三角形及理由;
(2)求OF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人以相同路线前往距离单位10km的培训中心参加学习.图中l甲、l乙分别表示甲、乙两人前往目的地所走的路程S(km)随时间t(分)变化的函数图象.以下说法:①乙比甲提前12分钟到达;②甲的平均速度为15千米/小时;③乙走了8km后遇到甲;④乙出发6分钟后追上甲.其中正确的有( ) 
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,二次函数y=﹣ ![]() x2+
x2+ ![]() x+2的图象与x轴交于点A,B(点B在点A的左侧),与y轴交于点C.过动点H(0,m)作平行于x轴的直线l,直线l与二次函数y=﹣
x+2的图象与x轴交于点A,B(点B在点A的左侧),与y轴交于点C.过动点H(0,m)作平行于x轴的直线l,直线l与二次函数y=﹣ ![]() x2+
x2+ ![]() x+2的图象相交于点D,E.
x+2的图象相交于点D,E.
(1)写出点A,点B的坐标;
(2)若m>0,以DE为直径作⊙Q,当⊙Q与x轴相切时,求m的值;
(3)直线l上是否存在一点F,使得△ACF是等腰直角三角形?若存在,求m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动:探究利用角的对称性构造全等三角形解决问题
(1)如图①,OP是∠MON的平分线,请你利用该图形画一对以OP所在直线为对称轴的全等三角形;(写出简单做法,不用证明两三角形全等,不用尺规作图亦可)
(2)如图②,在△ABC中,∠ACB=90°,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.请直接填空:∠AFE= 度,DF EF(填>,<或=);
(3)如图③,在△ABC中,如果∠ACB≠90°,而(2)中的其他条件不变,请问,你在(2)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,∠1=∠2,G是AD的中点,延长BG交AC于点E,F为AB上一点,CF⊥AD交AD于点H.下列说法:①AD是△ABE的角平分线;②BE是△ABD的边AD上的中线;③CH为△ACD的边AD上的高;④AH是△ACF的角平分线和高线.其中正确的有_______.
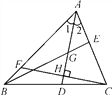
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正反比例函数的图像交于![]() 、
、![]() 两点,过第二象限的点
两点,过第二象限的点![]() 作
作![]() 轴,点
轴,点![]() 的横坐标为
的横坐标为![]() ,且
,且![]() ,点
,点![]() 在第四象限
在第四象限
(1)求这两个函数解析式;
(2)求这两个函数图像的交点坐标;
(3)若点![]() 在坐标轴上,联结
在坐标轴上,联结![]() 、
、![]() ,写出当
,写出当![]() 时的
时的![]() 点坐标
点坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知![]() ,
,![]() 分别为两坐标轴上的点,且
分别为两坐标轴上的点,且![]() ,
,![]() 满足
满足![]() ,且
,且![]() .
.
(1)求![]() 、
、![]() 、
、![]() 三点的坐标;
三点的坐标;
(2)若![]() ,过点
,过点![]() 的直线分别交
的直线分别交![]() 、
、![]() 于
于![]() 、
、![]() 两点,且
两点,且![]() ,设
,设![]() 、
、![]() 两点的横坐标分别为
两点的横坐标分别为![]() 、
、![]() ,求
,求![]() 的值;
的值;
(3)如图2,若![]() ,点
,点![]() 是
是![]() 轴上
轴上![]() 点右侧一动点,
点右侧一动点,![]() 于点
于点![]() ,在
,在![]() 上取点
上取点![]() ,使
,使![]() ,连接
,连接![]() ,当点
,当点![]() 在点
在点![]() 右侧运动时,
右侧运动时,![]() 的度数是否改变?若不变,请求其值;若改变,请说明理由.
的度数是否改变?若不变,请求其值;若改变,请说明理由.
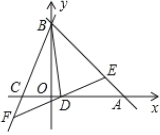
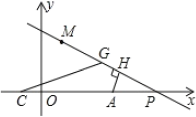
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的大致图象如图所示(1<x=h<2,0<xA<1).下列结论:①2a+b>0;②abc<0; ③若OC=2OA,则2b﹣ac=4; ④3a﹣c<0.其中正确的个数是( ) 
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com