
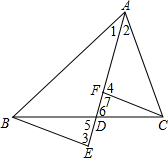
 如图,AD是△ABC的角平分线,BE⊥AD于E,CF⊥AD于F,求证:$\frac{AB}{AC}$=$\frac{DE}{DF}$.
如图,AD是△ABC的角平分线,BE⊥AD于E,CF⊥AD于F,求证:$\frac{AB}{AC}$=$\frac{DE}{DF}$. 分析 根据三角形角平分线定理得到$\frac{AB}{AC}=\frac{BD}{CD}$,又根据三角形相似得到$\frac{BD}{CD}=\frac{DE}{DF}$,于是得到结论.
解答 证明:∵AD是△ABC的角平分线,
∴$\frac{AB}{AC}=\frac{BD}{CD}$,
∵BE⊥AD于E,CF⊥AD于F,
∴∠3=∠7=90°,
∵∠5=∠6,
∴△BED∽△CFD,
∴$\frac{BD}{CD}=\frac{DE}{DF}$,
∴$\frac{AB}{AC}=\frac{DE}{DF}$.
点评 本题考查了三角形的角平分线定理,相似三角形的判定和性质,等量代换,熟练掌握三角形的角平分线定理是解题的关键.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
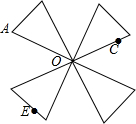 如图是一幅中心对称图形,请你找出点A绕点O旋转180°后的对应点B,定C的对应点D呢?你是怎么找到的?现在你能很快找到点E的对应点F吗?
如图是一幅中心对称图形,请你找出点A绕点O旋转180°后的对应点B,定C的对应点D呢?你是怎么找到的?现在你能很快找到点E的对应点F吗?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 必有两个不相等的实根 | B. | 没有实根 | ||
| C. | 必有两个相等的实根 | D. | 方程的根有可能取值a,b,c |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com