

| A. | 36 | B. | 40 | C. | 48 | D. | 50 |
分析 由图可知:第1个图形需要黑色棋子的个数是2×3-3=3,第2个图形需要黑色棋子的个数是3×4-4=8,第3个图形需要黑色棋子的个数是4×5-5=15,…按照这样的规律摆下去,则第n个图形需要黑色棋子的个数是(n+1)(n+2)-(n+2)=n2+2n.由此代入求得答案即可.
解答 解:∵第1个图形需要黑色棋子的个数是2×3-3=3,
第2个图形需要黑色棋子的个数是3×4-4=8,
第3个图形需要黑色棋子的个数是4×5-5=15,
…
∴第n个图形需要黑色棋子的个数是(n+1)(n+2)-(n+2)=n2+2n;
则第6个图形需要黑色棋子的个数是36+12=48.
故选:C.
点评 此题考查图形的变化规律,首先计算几个特殊图形,发现:数出每边上的个数,乘以边数再减去各个顶点的重复的点数,得出规律,解决问题.


科目:初中数学 来源: 题型:选择题
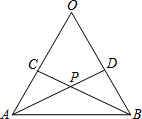 如图所示,AO=BO,CO=DO,连接AD、BC,设AD、BC相交于点P.结论:①△AOD≌△BOC;②△APC≌△BPD;③点P在∠AOB的平分线上.以上结论中( )
如图所示,AO=BO,CO=DO,连接AD、BC,设AD、BC相交于点P.结论:①△AOD≌△BOC;②△APC≌△BPD;③点P在∠AOB的平分线上.以上结论中( )| A. | 只有①正确 | B. | 只有②正确 | C. | 只有①②正确 | D. | ①②③都正确 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
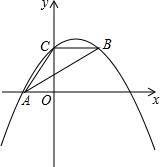 如图,抛物线y=ax2+bx+c经过A(-3.0)、C(0,4),点B在抛物线上,CB∥x轴,且AB平分∠CAO.
如图,抛物线y=ax2+bx+c经过A(-3.0)、C(0,4),点B在抛物线上,CB∥x轴,且AB平分∠CAO.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
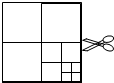 如图,将一张正方形纸片剪成四个小正方形,得到4个小正方形,称为第一次操作;然后,将其中的一个正方形再剪成四个小正方形,共得到7个小正方形,称为第二次操作;再将其中的一个正方形再剪成四个小正方形,共得到10个小正方形,称为第三次操作;…;根据以上操作,若操作670次,得到小正方形的个数是( )
如图,将一张正方形纸片剪成四个小正方形,得到4个小正方形,称为第一次操作;然后,将其中的一个正方形再剪成四个小正方形,共得到7个小正方形,称为第二次操作;再将其中的一个正方形再剪成四个小正方形,共得到10个小正方形,称为第三次操作;…;根据以上操作,若操作670次,得到小正方形的个数是( )| A. | 2009 | B. | 2010 | C. | 2011 | D. | 2012 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4cm、5cm、6cm | B. | 1cm、$\sqrt{2}$cm、3cm | C. | 2cm、3cm、4cm | D. | 1.5cm、2cm、2.5cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.237229×104 | B. | 23.7229×102 | C. | 2.37229×103 | D. | 237.229×101 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com