
 一枚质地均匀的正方体骰子六个面上标有数字1、2、3、4、5、6.随机抛掷这枚骰子一次,把着地一面的数字记做P点的横坐标,将该数的3倍记做P点的纵坐标.如图,抛物线y=-x2+4x+5与x轴负半轴交于点A,点B(4,5)在该抛物线上,则点P落在抛物线与直线AB围成的区域内(阴影部分,含边界)的概率是
一枚质地均匀的正方体骰子六个面上标有数字1、2、3、4、5、6.随机抛掷这枚骰子一次,把着地一面的数字记做P点的横坐标,将该数的3倍记做P点的纵坐标.如图,抛物线y=-x2+4x+5与x轴负半轴交于点A,点B(4,5)在该抛物线上,则点P落在抛物线与直线AB围成的区域内(阴影部分,含边界)的概率是
|
|
| 2 |
| 6 |
| 1 |
| 3 |
| 1 |
| 3 |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
| a4 |
| A、1个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
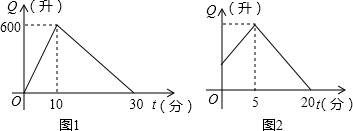
查看答案和解析>>
科目:初中数学 来源: 题型:
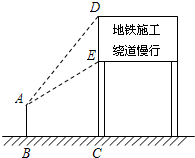 某市地铁工程正在加快建设,为了缓解市区内一些主要路段交通拥挤的现状,交警大队在一些主要路口设立了交通路况指示牌,如图所示,小明在离指示牌3.2米的点B处测得指示牌顶端D点和底端E点的仰角分别为52°和32°.求路况指示牌DE的高度.(精确到0.01米)
某市地铁工程正在加快建设,为了缓解市区内一些主要路段交通拥挤的现状,交警大队在一些主要路口设立了交通路况指示牌,如图所示,小明在离指示牌3.2米的点B处测得指示牌顶端D点和底端E点的仰角分别为52°和32°.求路况指示牌DE的高度.(精确到0.01米)查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com