
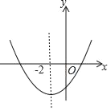
【题目】二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,顶点坐标为(﹣2,﹣9a),下列结论:①a﹣3b+2c>0;②3a﹣2b﹣c=0;③若方程a(x+5)(x﹣1)=﹣1有两个根x1和x2,且x1<x2,则﹣5<x1<x2<1;④若方程|ax2+bx+c|=1有四个根,则这四个根的和为﹣8.其中正确的结论有( )
A. 1个B. 2个C. 3个D. 4个
【答案】B
【解析】
根据二次函数的性质一一判断即可.
∵抛物线的开口向上,
∴a>0,
∵抛物线的顶点坐标(﹣2,﹣9a),
∴﹣![]() =﹣2,
=﹣2,![]() =﹣9a,
=﹣9a,
∴b=4a,c=﹣5a,
∴抛物线的解析式为y=ax2+4ax﹣5a,
∴a﹣3b+2c=a﹣12a﹣10a=﹣21a<0,所以①结论错误,
3a﹣2b﹣c=3a+4a+5a=12a>0,故②结论错误,
∵抛物线y=ax2+4ax﹣5a交x轴于(﹣5,0),(1,0),
∴若方程a(x+5)(x﹣1)=﹣1有两个根x1和x2,且x1<x2,则﹣5<x1<x2<1,正确,故结论③正确,
若方程|ax2+bx+c|=1有四个根,设方程ax2+bx+c=1的两根分别为x1,x2,
则![]() =﹣2,可得x1+x2=﹣4,
=﹣2,可得x1+x2=﹣4,
设方程ax2+bx+c=1的两根分别为x3,x4,则![]() =﹣2,可得x3+x4=﹣4,
=﹣2,可得x3+x4=﹣4,
所以这四个根的和为﹣8,故结论④正确,
故选B.


科目:初中数学 来源: 题型:
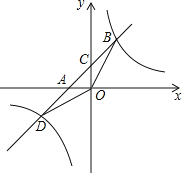
【题目】已知:如图,在平面直角坐标系xOy中,直线AB与x轴交于点A(﹣2,0),与反比例函数在第一象限内的图象的交于点B(2,n),连接BO,若S△AOB=4.
(1)求该反比例函数的解析式和直线AB的解析式;
(2)若直线AB与双曲线的另一交点为D点,求△ODB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
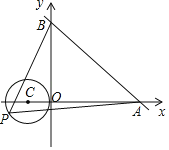
【题目】如图,直线y=﹣![]() x+6与x轴、y轴分别交于A、B两点,点P是以C(﹣1,0)为圆心,1为半径的圆上一点,连接PA,PB,则△PAB面积的最大值为_____.
x+6与x轴、y轴分别交于A、B两点,点P是以C(﹣1,0)为圆心,1为半径的圆上一点,连接PA,PB,则△PAB面积的最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,∠BAC>90°,点D为BC的中点,点E在AC上,将△CDE沿DE折叠,使得点C恰好落在BA的延长线上的点F处,连结AD,则下列结论不一定正确的是( )

A. AE=EF B. AB=2DE
C. △ADF和△ADE的面积相等 D. △ADE和△FDE的面积相等
查看答案和解析>>
科目:初中数学 来源: 题型:
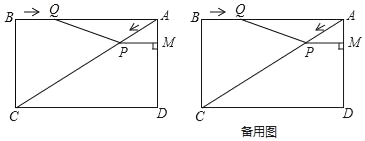
【题目】已知:如图,在矩形ABCD中,AC是对角线,AB=8cm,BC=6cm.点P从点A出发,沿AC方向匀速运动,速度为2cm/s,同时,点Q从点B出发,沿BA方向匀速运动,速度为2cm/s.过点P作PM⊥AD于点M,连接PQ,设运动时间为t(s)(0<t<4),解答下列问题:
(1)当t为何值时,点Q在线段AC的中垂线上;
(2)写出四边形PQAM的面积为S(cm2)与时间t的函数关系式;
(3)是否存在某一时刻t,使S四边形PQAM:S矩形ABCD=9:50?若存在,求出t的值;若不存在,请说明理由;
(4)当t为何值时,△APQ与△ADC相似.
查看答案和解析>>
科目:初中数学 来源: 题型:
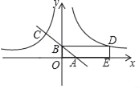
【题目】如图,一次函数y=﹣x+b交x轴于点A,交y轴于点B(0,1),与反比例函数![]() 的图象交于点C,C点的横坐标是﹣2.
的图象交于点C,C点的横坐标是﹣2.
(1)求反比例函数y1的解析式;
(2)设函数![]() 的图象与
的图象与![]() 的图象关于y轴对称,在
的图象关于y轴对称,在![]() 的图象上取一点D(D点的横坐标大于1),过D点作DE⊥x轴于点E,若四边形OBDE的面积为10,求D点的坐标.
的图象上取一点D(D点的横坐标大于1),过D点作DE⊥x轴于点E,若四边形OBDE的面积为10,求D点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
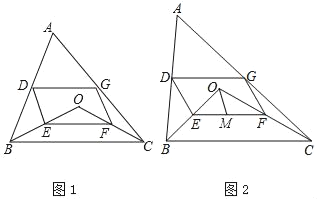
【题目】如图1,点D、E、F、G分别为线段AB、OB、OC、AC的中点.
(1)求证:四边形DEFG是平行四边形;
(2)如图2,若点M为EF的中点,BE:CF:DG=2:3:![]() ,求证:∠MOF=∠EFO.
,求证:∠MOF=∠EFO.
查看答案和解析>>
科目:初中数学 来源: 题型:
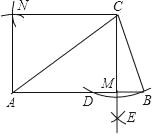
【题目】如图,已知等腰△ABC中,AB=AC.以C为圆心,CB的长为半径作弧,交AB于点D.分别以B、D为圆心,大于![]() BD的长为半径作弧,两弧交于点E.作射线CE交AB于点M.分别以A、C为圆心,CM、AM的长为半径作弧,两弧交于点N.连接AN、CN
BD的长为半径作弧,两弧交于点E.作射线CE交AB于点M.分别以A、C为圆心,CM、AM的长为半径作弧,两弧交于点N.连接AN、CN
(1)求证:AN⊥CN
(2)若AB=5,tanB=3,求四边形AMCN的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆慢车和一辆快车沿相同路线从A地到B地,所行驶的路程与时间的函数图象如图所示,下列说法正确的有()个
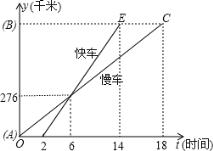
①快车追上慢车需6小时
②慢车比快车早出发2小时
③快车速度为46km/h
④慢车速度为46km/h
⑤AB两地相距828km
⑥快车14小时到达B地
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com