Question

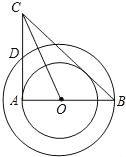
【题目】如图，在以O为圆心的两个同心圆中，AB经过圆心O，且与小圆相交于点A、与大圆相交于点B．小圆的切线AC与大圆相交于点D，且CO平分∠ACB．

（1）试判断BC所在直线与小圆的位置关系，并说明理由；

（2）试判断线段AC、AD、BC之间的数量关系，并说明理由；

（3）若AB=8cm，BC=10cm，求大圆与小圆围成的圆环的面积．（结果保留π）

Answer 1

【答案】（1）相切（2）AC+AD=BC（3）16π

【解析】

试题分析：（1）只要证明OE垂直BC即可得出BC是小圆的切线，即与小圆的关系是相切．

（2）利用全等三角形的判定得出Rt△OAD≌Rt△OEB，从而得出EB=AD，从而得到三者的关系是前两者的和等于第三者．

（3）根据大圆的面积减去小圆的面积即可得到圆环的面积．

试题解析：（1）BC所在直线与小圆相切．

理由如下：

过圆心O作OE⊥BC，垂足为E；

∵AC是小圆的切线，AB经过圆心O，

∴OA⊥AC；

又∵CO平分∠ACB，OE⊥BC，

∴OE=OA，

∴BC所在直线是小圆的切线．

（2）AC+AD=BC．

理由如下：

连接OD．

∵AC切小圆O于点A，BC切小圆O于点E，

∴CE=CA；

∵在Rt△OAD与Rt△OEB中，，

∴Rt△OAD≌Rt△OEB（HL），

∴EB=AD；

∵BC=CE+EB，

∴BC=AC+AD．

（3）∵∠BAC=90°，AB=8cm，BC=10cm，

∴AC=6cm；

∵BC=AC+AD，

∴AD=BC﹣AC=4cm，

∵圆环的面积为：S=π（OD）2﹣π（OA）2=π（OD2﹣OA2），

又∵OD2﹣OA2=AD2，

∴S=42π=16π（cm2）．