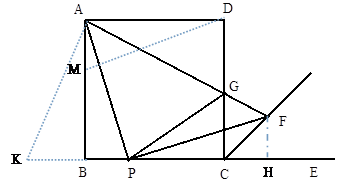
试题分析::(1)过点F作FH⊥BE于点H,利用正方形的性质,证得△BAP≌△HPF得出PH=AB,BP=FH进一步得出BP+PC=PC+CH,CH=BP=FH,∠FHC=90°,求得∠DCF=90°-45°=45°得出结论;
(2)延长PB至K,使BK=DG,连接AK,证得△ABK≌△ADG和△KAP≌△GAP,找出边相等得出结论;
(3)首先判定存在,在直线AB上取一点M,使四边形DMPF是平行四边形,证得△ABP≌△DAM,进一步球的结论即可.
(1)证明:过点F作FH⊥BE于点H,
∵四边形ABCD是正方形,
∴∠ABC=∠PHF=∠DCB=90º,AB=BC,
∴∠BAP+∠APB=90º
∵AP⊥PF,
∴∠APB+∠FPH=90º
∴∠FPH=∠BAP
又∵AP=PF
∴△BAP≌△HPF
∴PH=AB,BP=FH
∴PH="BC"
∴BP+PC=PC+CH
∴CH="BP=FH"
而∠FHC=90º. ∴∠FCH=CFH=45º
∴∠DCF=90º-45º=45º
∴∠GCF=∠FCE
(2)PG=PB+DG
证明:延长PB至K,使BK=DG,
∵四边形ABCD是正方形
∴AB="AD," ∠ABK=ADG=90º
∴△ABK≌△ADG
∴AK="AG," ∠KAB=∠GAD,
而∠APF="90" º,AP=PF
∴∠PAF=∠PFA="45" º
∴∠BAP+∠KAB=∠KAP="45" º=∠PAF
∴△KAP≌△GAP
∴KP=PG,
∴KB+BP=DG+BP=PG
即,PG=PB+DG
(3)存在.
如图,在直线AB上取一点M,使四边形DMPF是平行四边形,
则MD∥PF,且MD=FP,
又∵PF=AP,
∴MD=AP
∵四边形ABCD是正方形 ,
∴AB=AD,∠ABP=∠DAM
∴△ABP≌△DAM
∴AM=BP=2,
∴BM=AB-AM=5-2="3."
∴当BM=3,BM+AM=AB时,四边形DMPF是平行四边形.

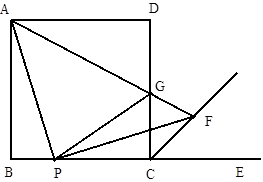



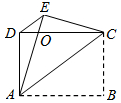


 ,求△BDE的周长;
,求△BDE的周长;