
分析 (1)直接利用有理数加减运算法则化简求出即可;
(2)直接利用有理数除法运算法则化简求出即可;
(3)直接利用二次根式以及立方根的性质、绝对值的性质化简求出即可;
(4)直接利用乘方以及有理数乘除运算法则化简求出即可.
解答 解:(1)-20+14-18+13
=-6-18+13
=-24+13
=-11;
(2)(-$\frac{3}{4}$+$\frac{7}{12}-\frac{5}{9}$)$÷(-\frac{1}{36})$
=(-$\frac{3}{4}$+$\frac{7}{12}-\frac{5}{9}$)×(-36)
=27-21+20
=26;
(3)$\root{3}{-64}$+$\sqrt{\frac{16}{9}}$-|-3|
=-4+$\frac{4}{3}$-3
=-5$\frac{2}{3}$;
(4)-23×(-1$\frac{1}{2}$)2+5×(-6)-(-4)3÷8
=-8×$\frac{9}{4}$-30+64÷8
=-18-30+8
=-40.
点评 此题主要考查了实数运算,正确利用相关性质化简各数是解题关键.


科目:初中数学 来源: 题型:填空题
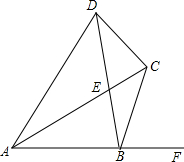 已知:AB=2,AC平分∠DAB,∠DAB+∠DCB=180°,∠DCB=120°,当∠ABD=∠CBF时,则AC=$\sqrt{3}$+1.
已知:AB=2,AC平分∠DAB,∠DAB+∠DCB=180°,∠DCB=120°,当∠ABD=∠CBF时,则AC=$\sqrt{3}$+1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
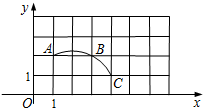 如图,在平面直角坐标系中,网格中小正方形的边长为1个单位长度,过格点A,B,C作一圆弧.
如图,在平面直角坐标系中,网格中小正方形的边长为1个单位长度,过格点A,B,C作一圆弧.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
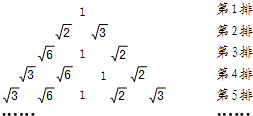 如图将1、$\sqrt{2}$、$\sqrt{3}$、$\sqrt{6}$按下列方式排列.若规定(m,n)表示第m排从左向右第n个数,则(5,4)与(15,8)表示的两数之积是( )
如图将1、$\sqrt{2}$、$\sqrt{3}$、$\sqrt{6}$按下列方式排列.若规定(m,n)表示第m排从左向右第n个数,则(5,4)与(15,8)表示的两数之积是( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{6}$ | D. | 3$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若a≠b,则a2=b2 | B. | 若a2=b2,则a≠b | C. | 若a=b,则a2≠b2 | D. | 若a2=b2,则a=b |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com