
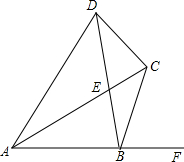
 已知:AB=2,AC平分∠DAB,∠DAB+∠DCB=180°,∠DCB=120°,当∠ABD=∠CBF时,则AC=$\sqrt{3}$+1.
已知:AB=2,AC平分∠DAB,∠DAB+∠DCB=180°,∠DCB=120°,当∠ABD=∠CBF时,则AC=$\sqrt{3}$+1. 分析 先证明A、B、C、D四点共圆,由圆周角定理得出∠ABD=∠ACD,再由已知条件和圆内接四边形的性质得出∠ACD=∠ADC,由三角形内角和定理求出∠ACD=∠ADC=75°,得出∠ACB=45°,作BM⊥AC于M,则∠AMB=∠CMB=90°,由含30°角的直角三角形的性质和勾股定理得出BM=$\frac{1}{2}$AB=1,AM=$\sqrt{3}$,得出△CBM是等腰直角三角形,因此CM=BM=1,即可得出AC的长.
解答 解:∵∠DAB+∠DCB=180°,
∴A、B、C、D四点共圆,∠DAB=180°-∠DCB=60°,
∴∠ABD=∠ACD,
∵∠ABD=∠CBF,
∴∠ACD=∠CBF,
∵∠CBF=∠ADC,
∴∠ACD=∠ADC,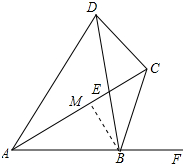
∵AC平分∠DAB,
∴∠DAC=∠BAC=30°,
∴∠ACD=∠ADC=75°,
∴∠ACB=120°-75°=45°,
作BM⊥AC于M,如图所示:
则∠AMB=∠CMB=90°,
∴BM=$\frac{1}{2}$AB=1,△CBM是等腰直角三角形,
∴AM=$\sqrt{3}$BM=$\sqrt{3}$,CM=BM=1,
∴AC=AM+CM=$\sqrt{3}$+1;
故答案为:$\sqrt{3}$+1.
点评 本题是四点共圆综合题目,考查了四点共圆、圆周角定理、三角形内角和定理、圆内接四边形的性质、含30°角的直角三角形的性质、勾股定理、等腰直角三角形的判定与性质等知识;本题综合性强,有一定难度,证明四点共圆和作辅助线运用特殊直角三角形的性质是解决问题的关键.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:填空题
 实数a,b,c在数轴上对应点的位置如图所示,则$\root{3}{{a}^{3}}$+|a+b|-$\sqrt{(c-a)^{2}}$+|b-c|=a-2b.
实数a,b,c在数轴上对应点的位置如图所示,则$\root{3}{{a}^{3}}$+|a+b|-$\sqrt{(c-a)^{2}}$+|b-c|=a-2b.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x+2)2=3 | B. | (x+2)2=-5 | C. | (x+2)2=-3 | D. | (x+4)2=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
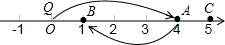 如图,数轴上一电子跳蚤Q从原点0出发,第1次沿数轴向右跳4个单位长度落在点A,第2次从点A出发沿数轴向左跳3个单位长度落在点B,第3次从点B沿数轴向右跳4个单位长度落在点C,第4次从点C出发沿数轴向左跳3个单位长度落在点D,…,按此规律继续跳动.
如图,数轴上一电子跳蚤Q从原点0出发,第1次沿数轴向右跳4个单位长度落在点A,第2次从点A出发沿数轴向左跳3个单位长度落在点B,第3次从点B沿数轴向右跳4个单位长度落在点C,第4次从点C出发沿数轴向左跳3个单位长度落在点D,…,按此规律继续跳动.查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 伦敦时间2015年9月16日11时 | B. | 巴黎时间2015年9月16日13时 | ||
| C. | 智利时间2015年9月16日5时 | D. | 曼谷时间2015年9月16日18时 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com