
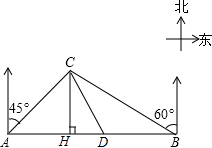
 某大草原上有一条笔直的公路,在紧靠公路相距40千米的A、B两地,分别有甲、乙两个医疗站,如图,在A地北偏东45°,B地北偏西60°方向上有一牧民区C,过点C作CH⊥AB于H.
某大草原上有一条笔直的公路,在紧靠公路相距40千米的A、B两地,分别有甲、乙两个医疗站,如图,在A地北偏东45°,B地北偏西60°方向上有一牧民区C,过点C作CH⊥AB于H.分析 (1)设CH为未知数,分别表示出AH,BH的值,让其相加得40求值即可求得CH的长,进而可求得CB的长;
(2)由CD和BC的数量关系可得CD和CH的数量关系,进而可得HD的长,让BH的长减去DH的长即为BD的距离.
解答 解:(1)设CH为x千米,由题意得,∠CBH=30°,∠CAH=45°,
∴AH=CH=x,
在Rt△BCH中,tan30°=$\frac{x}{BE}$,
∴BH=$\sqrt{3}$x,
∵AH+HB=AB=40,
∴x+$\sqrt{3}$x=40,
解得x=20$\sqrt{3}$-20,
∴CB=2CH=40$\sqrt{3}$-40.
答:牧民区C到B地的距离为(40$\sqrt{3}$-40)千米;
(2)∵C、D 两地距离是B、C两地距离的$\frac{\sqrt{3}}{2}$倍,CH=$\frac{1}{2}$BC,
∴DC=$\frac{\sqrt{3}}{2}$(40$\sqrt{3}$-40)=60-20$\sqrt{3}$,BH=$\sqrt{3}$x=$\sqrt{3}$(20$\sqrt{3}$-20)=60-20$\sqrt{3}$,
∴DH=$\sqrt{2}$CH=20$\sqrt{6}$-20$\sqrt{2}$,
∴BD=BH-DH=(60-20$\sqrt{3}$)-(20$\sqrt{6}$-20$\sqrt{2}$)=60-20$\sqrt{3}$-20$\sqrt{6}$+20$\sqrt{2}$≈4.7.
答:BD之间的距离为4.7千米.
点评 本题考查了解直角三角形的应用;构造直角三角形,利用勾股定理及特殊的三角函数值求解是解决本题关键.


 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:填空题
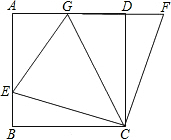 如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,G在AD上,且DF=BE.①CE=CF;②EC⊥CF;③△ECG≌△FCG,④若∠GCE=45°,则EG=BE+GD,以上说法正确的是①②④.
如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,G在AD上,且DF=BE.①CE=CF;②EC⊥CF;③△ECG≌△FCG,④若∠GCE=45°,则EG=BE+GD,以上说法正确的是①②④.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com